기초 금융수학 17-옵션(1)
옵션:
구매자에게 특정 상품을 특정 가격에 특정일 또는 그 이전에 사거나 팔 수 있는 권리를 부여하는 계약
옵션은 금, 밀, 튤립, 외환, 영화대본, 주식 등 다양한 제품에 대해 작성된다.
예: 금 소유자는 다음 30일 이내에 특정 가격에 구매할 권리를 팔 수 있고, 옵션 보유자는 권리행사를 안해도 된다. 그러나 구매자가 권리를 행사하면 판매자는 금을 팔아야 한다.
행사가격(exercise(strike) price): 미리 정한 가격, 특정 가격
만기일(maturity(expiration) price): 미래 일정 시점, 특정 일
프리미엄(premium): 옵션 매수자가 선택의 대가로 지불하는 옵션 구입가격(option price)
내가격(in-the-money): 옵션을 행사해 프리미엄을 제외하고 발생한 수익
등가격(at-the-money): 자산의 가격이 행사가격과 같을 때의 옵션 구입가격
외가격(out-the-money): 옵션을 행사했을 때 수익이 남지 않을 때의 옵션 구입가격
*여기서는 주식 옵션을 다룰 것이다. 옵션은 보유자에게 주식을 특정한 기간 동안 특정한 가격에 팔거나 사는 권리를 부여한다. 그러므로 옵션 구매자는 주식으 팔거나 사는 권리를 갖지만 의무는 지지 않는다. 옵션 판매자(발행자)는 옵션이 행사되면 주식을 팔거나 사야 한다.
아메리칸 옵션(American option):
보유자에게 행사가격이라 부르는 특정 가격에 만기일이라 부르는 특정일 또는 그 이전에 자산을 사거나 팔 권리를 부여한다. 미국, 홍콩, 싱가포르, 영국에서 발행한다.
유러피언 옵션(European option):
같은 권리를 부여하나 옵션을 만기일에만 행사할 수 있다. 한국, 독일, 프랑스에서 발행한다.
버뮤다형 옵션(Bermudian option):
만기일 이전 특정일에 행사할 수 있다. 케이맨제도와 스위스에서 발행한다.
아시안 옵션(Asian option):
옵션 기간 내의 자산 가격의 평균이 행사가격이다. 일본에서 발행한다.
*아메리칸, 유러피언이라는 용어는 옵션의 형태를 지칭하는 것이지 옵션이 거래되는 지리학적 장소를 말하는 것이 아니다.
콜옵션(call option): 자산을 특정가격(행사가격)에 살 권리
풋옵션(put option): 자산을 특정가격에 팔 권리
| 콜옵션 | 풋옵션 | |
| 내가격 | \(S>X\) | \(S<X\) |
| 등가격 | \(S=X\) | \(S=X\) |
| 외가격 | \(S<X\) | \(S>X\) |
이 표에서 \(S\)는 주가, \(X\)는 행사가격이다.
옵션이 외가격(행사시 수익 없음)이면, 내가격일 때에 비해 낮아진다. 콜옵션의 경우, 주식가격이 행사가격보다 낮으면 옵션은 외가격이다. 주식가격이 행사가격보다 훨씬 낮으면 옵션은 쓸모없어 만료될 가능성이 매우 높고, 특히 만기일이 가까우면 더욱 그렇다. 이 경우 옵션의 가격은 낮아진다.
옵션이 내가격(행사시 수익 있음)이면, 옵션의 가치는 높아지는데 콜옵션 만기일에 가까워질수록 옵션 가격이 더 낮아진다는 것을 유의해야 한다.
정리 10.1(콜옵션과 풋옵션의 가격정리) 다음을 가정하자.
1. 거래 비용이 없다.
2. 콜옵션, 풋옵션 둘 다 주식을 주어진 가격에 구입할 수 있다.
\(T\)를 만료시점, \(X\)를 행사가격, \(S(T)\)를 \(T\)시점에서의 주식가격, \(C(T)\), \(P(T)\)를 각각 \(T\)시점에서의 주당 콜옵션과 풋옵션 가격이라고 하자. 그러면 다음 식이 성립한다.$$\begin{align*}C(T)&=\begin{cases}0&\,(S(T)\leq X)\\S(T)-X&\,(S(T)>X)\end{cases}\\P(T)&=\begin{cases}0&\,(S(T)\geq X)\\X-S(T)&\,(S(T)<X)\end{cases}\end{align*}$$
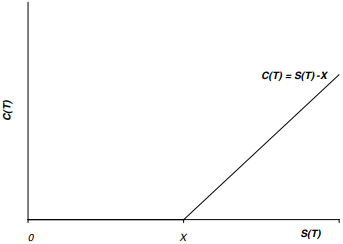
증명: 콜옵션에 대해 증명하자.
옵션이 외가격(\(S(T)\leq X\))이면 투자자는 콜옵션을 구매하려 하지 않으므로 \(S(T)<X\)이면 \(C(T)=0\)이다.
이제 만기일 직전에 콜옵션의 가격이 \(C(T)\), 기초 주식의 가격을 \(S(T)\)라 하자. 가능한 경우는 다음의 세 가지 경우 중 하나이다.$$C(T)<S(T)-X,\,C(T)>S(T)-X,\,C(T)=S(T)-X$$ \(C(T)<S(T)-X\)이면 투자자는 콜옵션을 구매해 \(X\)에 행사하여 주식을 구입하고 이를 \(S(T)\)에 팔아 \(S(T)-C(T)-X\)만큼 수익을 남기나 이런 상황은 지속될 수 없다.
\(C(T)>S(T)-X\)이면 \(C(T)+X>S(T)\)이므로 콜옵션을 구매하여 행사하는 비용 \(C(T)+X\)가 주식 가격보다 높으므로 주식을 원하는 투자자는 콜옵션을 구매하지 않을 것이다.
그러므로 \(S(T)>X\)이면 \(C(T)=S(T)-X\)이다.
풋옵션도 이와 같은 방법으로 보일 수 있다. 옵션이 내가격(\(S(T)\leq X\))일 때 투자자는 풋옵션을 구매하려 한다(\(X-S(T)\)의 이득).
\(P(T)<X-S(T)\)이면 투자자는 풋옵션과 주식을 구매해 \(X\)에 팔아 \(X-P(T)-S(T)\)의 이익을 보나 이런 상황은 지속될 수 없다.
\(P(T)>X-S(T)\)이면 풋옵션과 주식을 구매하는 비용이 행사가격 \(X\)보다 높아 풋옵션을 구매하지 않을 것이다. 그러므로 \(S(T)\leq X\)일 때 \(P(T)=X-S(T)\)이다.
\(S(T)\geq X\)이면(외가격), 투자자는 풋옵션을 구매하려 하지 않으므로 이때 \(P(T)=0\)이다.
프리미엄(옵션 구입가격)에 영향을 끼치는 것에는 기초 주식의 가격, 만기일까지 남은 기간, 주식 수익의 변동성(이 중에 연속복리로 계산한 주식 수익률의 분산도 있다)을 포함한 여러 요인들이 있다.
만기일까지 남은 기간이 특히 중요하다. 옵션이 내가격이면 옵션의 내재가치는 주식 가격과 행사가격의 차로 정의된다. 옵션이 외가격이면 내재가치는 0이다. 시간가치는 프리미엄과 내재가치의 차이다. 그러므로 프리미엄은 옵션의 내재가치와 시간가치의 합과 같다.
예: 주식가격이 주당 35달러, 대응하는 콜옵션의 행사가격이 30달러, 콜 프리미엄이 7달러이면, 내재가치는 35$-30$=5달러, 시간가치는 7$-5$=2달러이다.
투자자가 옵션 포지션을 취한 다음에는 다음의 세 가지 선택이 가능하다.
1. 포지션을 청산한다. 옵션 발행자(판매자)는 시장에서 옵션을 재구입할 수 있고, 옵션 구매자는 계약을 판매할 수 있다. 두 경우 모두 이러한 거래는 상쇄하는 거래로 투자자의 옵션 포지션은 종료된다. 이것은 유러피언 옵션의 보유자가 만료되기 전에 이 자산을 처분할 수 있는 유일한 방법이다.
2. 포지션을 유지한다. 옵션이 외가격(행사시 수익X)으로 만료되면, 옵션 발행자는 프리미엄을 실현해 (수수료를 뺀) 수익을 취할 것이다.
3. 옵션을 행사한다. 예를들어 콜옵션 구매자가 행사가격에 주식을 구매한다. 옵션발행자는 주식을 행사가격에 매도한다.
어느 회사의 주식이 주당 \(S(t)\)에 거래되고 있다고 하고, 시간 \(t(0\leq t\leq T)\)에 대응하는 콜옵션 가격이 \(C(t)\), 풋옵션 가격이 \(P(t)\), 행사가격이 \(X\)라 하자.
실제로 투자자가 음의 금액에 해당하는 자산을 팔지 않으므로 \(S(t)\geq0\), \(X\geq0\), \(C(t)\geq0\), \(P(t)\geq0\)으로 가정하고 다음의 관계가 성립함을 보이기로 한다.$$C(t)\geq S(t)-X\,(1),\,P(t)\geq X-S(t)\,(2)$$ 위 두 식의 증명은 차익거래라는 개념을 이용한다. 차익거래(arbitrage)는 양의 확률로 수익을 낳는 무위험(no risk), 무순투자(no net investment) 전략이다.
달리 말하면 차익거래란 "공짜점심"에 해당하는 투자이다. 실제로는 차익거래 상황이 오래 유지될 수 없으므로 차익거래는 발생할 수 없다고 가정한다.
식 (1)의 증명: \(S(t)\leq X\)이면 \(S(t)-X\leq 0\)이고 \(C(t)\geq0\)이므로 (1)은 성립한다.
\(S(t)>X\)라 하자. \(C(t)<S(t)-X\)라 하여 이것에서 차익거래가 발생함을 보임으로써 모순을 도출한다. \(S(t)>X\)이고 \(C(t)<S(t)-X\)이면 투자자는 콜옵션을 \(C(t)\)에 구입하고 \(X\)에 행사해 주식을 얻은 다음, 이 주식을 \(S(t)\)에 판다. 그러면 투자자의 수익은 \(C(t)+X<S(t)\)이므로 \(S(t)-C(t)-X>0\)이다. 거래가 이루어질 수 있다고 하고 거래 비용이 없다고 하면 투자자는 위험이 없고 순 기회비용도 없는, 즉 차익거래가 가능하다는 것인데 이는 불가능하다.
식 (2)의 증명: \(S(t)\geq X\)이면 \(X-S(t)\leq0\)이고 \(P(t)\geq0\)이므로 (2)는 성립하다.
\(S(t)<X\)라 하자. \(P(t)<X-S(t)\)라 하여 이곳에서 차익거래가 발생함을 보인다.
\(S(t)<X\)이고 \(P(t)<X-S(t)\)이면 투자자는 풋옵션과 주식을 얻은 다음 \(X\)에 행사한다. 그러면 투자자의 수익은 \(P(t)+S(t)<X\)이므로 \(X-P(t)-S(t)>0\)이다. 거래가 이루어질 수 있다고 하고 거래 비용이 없다고 하면 차익거래가 가능한데 이는 불가능하다.
참고자료:
An Introduction to the Mathematics of Money Saving and Investing, Lovelock, Mendel, Wright, Springer
'확률및통계 > 기초 금융수학' 카테고리의 다른 글
| 기초 금융수학 19-옵션(3) (0) | 2022.10.31 |
|---|---|
| 기초 금융수학 18-옵션(2) (0) | 2022.10.28 |
| 기초 금융수학 16-주식, 가격, 위험(3) (0) | 2022.10.24 |
| 기초 금융수학 15-주식, 가격, 위험(2) (1) | 2022.10.23 |
| 기초 금융수학 14-주식, 가격, 위험(1) (0) | 2022.10.23 |
