기초 금융수학 12-채권(4)
수익률이 같은 채권에 대해 다음의 변화율 값의 절댓값이 더 크면 더 위험함을 보였다.$$\frac{P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})}{P(y^{(m)})}$$ 국소적 선형성(local linearity), 즉 테일러 전개의 처음 두 항$$P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})\approx\Delta y^{(m)}P'(y^{(m)})$$을 이용하여 다음 식이 성립함을 보였다.$$\frac{P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})}{P(y^{(m)})}\approx-\Delta y^{(m)}v\,\left(v=-\frac{P'(y^{(m)}}{P(y^{(m)}}\right)$$(여기서 \(v\)는 수정 듀레이션이다) 일반적으로 \(\Delta y^{(m)}>0\)이면, \(v\)의 정의에서 넣은 음(-)의 부호로 인해 수정 듀레이션이 더 크면 채권은 더 위험하다.
두 채권이 같은 수익률과 수정 듀레이션을 갖는다고 하면$$P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})\approx \Delta y^{(m)}P'(y^{(m)})+\frac{1}{2}(\Delta y^{(m)})^{2}P''(y^{(m)})$$이므로$$\frac{P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})}{P(y^{(m)})}\approx-\Delta y^{(m)}v+\frac{1}{2}(\Delta y^{(m)})^{2}P''(y^{(m)})C\,\left(C=\frac{P''(y^{(m)})}{P(y^{(m)})}\right)$$이고 여기서 \(C\)를 채권의 볼록성(convexity)이라고 한다. 그러므로 같은 수익률과 같은 수정 듀레이션을 갖는 채권에 대해 \(\Delta y^{(m)}>0\)이면, 볼록성이 더 커질수록 채권은 더 위험해진다. 실제로 \(C\)는 다음과 같이 주어진다.$$C=\frac{r\sum_{k=1}^{n}{k(k+1)(1+y)^{-k}}+n(n+1)(1+y)^{-n}}{(1+y)^{2}\left\{r\sum_{k=1}^{n}{(1+y)^{-k}}+(1+y)^{-n}\right\}}$$ 용어 "볼록성, 2차미분, 곡률(curvature)"을 서로 바꾸어 쓸 수 없다는 것을 아는 것이 중요하다. 함수의 볼록성, 2차미분 어느 것도 얼마나 함수(그래프)가 "휘는 지" 잴 수 없다는 것이다.
다음과 같이 정의되는 \(P(y^{(m)})\)의 곡률 \(\kappa\)는 구부러진(휜) 정도를 잰다.$$\kappa=\frac{P''(y^{(m)})}{[1+\{P'(y^{(m)})\}^{2}]^{\frac{3}{2}}}$$ 여러 자산에 걸쳐 투자를 다양화 하는 것이 신중한 태도이다. 분별 있는 투자자는 여러 채권으로 구성된 포트폴리오를 보유한다. 포트폴리오 가치의 이자에 대한 민감도를 측정하기로 한다. 채권 하나인 경우와 같이 포트폴리오 민감도로 적절한 척도는 듀레이션이다.
포트폴리오사 \(1\leq j\leq J\)에 대해 각각 만기 \(\displaystyle\frac{n_{j}}{m}\), 가격 \(P_{j}\), 듀레이션 \(d_{j}\)인 \(J\)개의 채권으로 구성되었다고 하자. 각 채권에 대해 기간당 수익률은 \(y\)이고, 연간 이자 지급횟수는 \(m\)이다.
포트폴리오의 듀레이션을 계산하는 방법에는 두 가지 방법이 있다.
1. 포트폴리오의 듀레이션은 포트폴리오를 구성하는 채권의 듀레이션의 가중평균으로, 가중치는 채권의 시장가치(가격)의 포트폴리오 전체의 시장가치에 대한 비율이다. 그러므로 \(C_{k_{j}}\)가 채권 \(j\)에 대해 기간 \(k\)에 대한 현금흐름이면(채권에 대한 현금흐름은 액면가와 액면이자율에 의해 결정되는 이자 지급이다) 포트폴리오의 듀레이션 \(D\)는 다음과 같다.$$D=\sum_{j=1}^{J}{\left(\frac{P_{j}}{\sum_{j=1}^{J}{P_{j}}}\right)d_{j}}=\frac{\sum_{k=1}^{n}{P_{j}d_{j}}}{\sum_{j=1}^{J}{P_{j}}}\,\left(P_{j}=\sum_{k=0}^{n_{j}}{C_{k_{j}}(1+y)^{-k}},\,d_{j}=\frac{\sum_{k=0}^{n_{j}}{kC_{k_{j}}(1+y)^{-k}}}{m\sum_{k=0}^{n_{j}}{C_{k_{j}}(1+y)^{-k}}}\right)$$예: 채권 1(액면가 10,000달러, 액면이자율 5%, 만기 2년 채권)과 채권 2(액면가 20,000달러, 액면이자율 8%, 만기 3년 채권)로 구성된 포트폴리오를 생각하자. 수익률이 현재 7%이면 채권 1의 시장가치는$$P_{1}=10000\left\{0.025\frac{1-(1+0.035)^{-4}}{0.035}+(1+0.035)^{-4}\right\}=9,632.69\$ $$이고, 채권 2의 시장가치는$$P_{2}=20000\left\{0.04\frac{1-(1+0.035)^{-6}}{0.035}+(1+0.035)^{-6}\right\}=20,532.86\$ $$이다. 따라서 포트폴리오의 시장가치는 다음과 같다.$$P_{1}+P_{2}=9,632.69+20,532.86=30,165.55\$ $$채권 1의 듀레이션은$$d_{1}=-\frac{1}{0.035\times2}\frac{0.025\{1+0.035+4\times0.035-(1+0.035)^{4+1}\}-4\times0.035^{2}}{0.025\{(1+0.035)^{4}-1\}+0.035}=1.926$$채권 2의 듀레이션은$$d_{1}=-\frac{1}{0.035\times2}\frac{0.04\{1+0.035+6\times0.035-(1+0.035)^{6+1}\}-6\times0.035^{2}}{0.04\{(1+0.035)^{6}-1\}+0.035}=2.730$$이므로 따라서 포트폴리오의 듀레이션 \(D\)는 다음과 같다.$$D=\frac{P_{1}d_{1}+P_{2}d_{2}}{P_{1}+P_{2}}=2.473$$2. 포트폴리오의 듀레이션을 계산하는 두 번째 방법은 포트폴리오를 구성하는 채권의 현금흐름이 결합되어 듀레이션 계산공식에 따라 하나의 현금흐름 연쇄에 적용된다. 그러므로 포트폴리오의 듀레이션은 다음과 같다.$$D=\frac{\sum_{k=0}^{n}{k(1+y)^{-k}}\sum_{j=1}^{J}{C_{k_{j}}}}{m\sum_{k=0}^{n}{(1+y)^{-k}}\sum_{j=1}^{J}{C_{k_{j}}}}\,\left(n=\max_{1\leq j\leq J}{n_{j}},\,k>n_{j}\,\Rightarrow\,C_{k_{j}}=0\right)$$앞의 예에서 채권 1의 현금흐름은

이고, 채권 2의 현금흐름은

이므로 다음과 같은 시간도표가 만들어진다.

이 현금흐름들을 결합하면 다음과 같다.

듀레이션 공식에 대입하기 위해 다음 표를 작성한다.

이 표로부터 듀레이션이 \(\displaystyle\frac{149226.50}{230165.55}=2.473\)이 됨을 알 수 있고, 앞의 예와 같은 값이다.
*이 두 방법은 다음에 의해 같다.
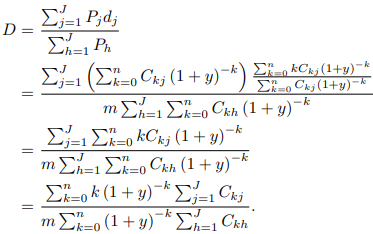
참고자료:
An Introduction to the Mathematics of Money Saving and Investing, Lovelock, Mendel, Wright, Springer
'확률및통계 > 기초 금융수학' 카테고리의 다른 글
| 기초 금융수학 14-주식, 가격, 위험(1) (0) | 2022.10.23 |
|---|---|
| 기초 금융수학 13-주식과 주식시장 (1) | 2022.10.14 |
| 기초 금융수학 11-채권(3) (1) | 2022.10.07 |
| 기초 금융수학 10-채권(2) (1) | 2022.10.06 |
| 기초 금융수학 9-채권(1) (1) | 2022.10.05 |
