기초 금융수학 11-채권(3)
두 채권을 수익률 변화에 대한 가격 민감도를 가지고 두 채권을 비교할 수도 있다. 다시 말하면 수익률 \(y^{(m)}\)이 \(\Delta y^{(m)}\)만큼 바뀌면 백분율 가격변화(percent price change)가 어느 정도 영향을 받는지 비교할 수 있다. 그러므로 백분율 가격 변화$$\frac{P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})}{P(y^{(m)})}$$를 각 채권에 대해 계산하고, 수익률이 같은 채권들에서 이 값의 절댓값이 더 큰 채권이 더 위험하다.
예: 20년 만기 9% 만기 상환채와 15년 만기 7% 만기 상환채의 만기 수익률이 모두 6%이다. 수익률이 1% 증가할 때 위험한 것은?
답: \(y^{(m)}=0.06\), \(\Delta y^{(m)}=0.01\)이므로 백분율 가격변화는 다음과 같다.$$\frac{P((0.06+0.01)-P(0.06)}{P(0.06)}=\frac{P(0.07)}{P(0.06)}-1$$ 첫째 채권에 대해 \(m=2\), \(\displaystyle r=\frac{0.09}{2}=0.045\), \(n=2\times20=40\)이고$$P(y^{(m)})=100\left\{0.045\frac{1-\left(1+\frac{y^{(m)}}{2}\right)^{-40}}{\frac{y^{(m)}}{2}}+\left(1+\frac{y^{(m)}}{2}\right)^{-40}\right\}$$이므로 \(P(0.06)=134.672\), \(P(0.07)=121.355\)이고 첫째 채권에 대해 \(\displaystyle\frac{P(0.07)}{P(0.06)}-1=-0.0989\)이다. 이것은 수익률 1% 증가에 대한 백분율 가격 변화가 약 9.9% 감소를 뜻한다.
둘째 채권에 대해 \(m=2\), \(\displaystyle r=\frac{0.07}{2}=0.035\), \(n=2\times15=30\)이고 같은 방법으로 \(P(0.06)=109.8\), \(P(0.07)=100\)이므로 \(\displaystyle\frac{P(0.07)}{P(0.06)}-1=-0.0893\)이다. 이것은 수익률 1% 증가에 대한 백분율 가격 변화가 약 8.9% 감소를 뜻한다.
그러므로 첫째 채권이 둘째 채권보다 더 위험하다.
국소적 선형성(local linearity)에서 다음의 근사식이 작은 \(\Delta y^{(m)}\)에 대해 성립하고$$\frac{P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})}{P(y^{(m)})}\approx\Delta y^{(m)}\frac{dP}{dy^{(m)}}$$이를 다음과 같이 나타낼 수 있다.$$\frac{P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})}{P(y^{(m)})}\approx\Delta y^{(m)}\frac{P'(y^{(m)})}{P(y^{(m)})}$$ \(P(y^{(m)})>0\), \(P'(y^{(m)})<0\)이므로 백분율 가격 변화의 부호는 \(y^{(m)}\)의 변화의 부호와 반대이다. 일반적으로 수정 듀레이션(modified duration)을 다음과 같이 정의하고$$v=-\frac{P'(y^{(m)})}{P(y^{(m)})}$$음의 부호는 \(v\)가 양수가 되기 위해 도입한 것이고 단위는 시간이다. 이 정의에서 다음의 근사식이 성립한다.$$\frac{P(y^{(m)}+\Delta y^{(m)})-P(y^{(m)})}{P(y^{(m)})}\approx\Delta y^{(m)}v$$ \(\displaystyle y=\frac{y^{(m)}}{m}\)이므로$$P(y^{(m)})=100\left\{r\frac{1-(1+y)^{-n}}{y}+(1+y)^{-n}\right\}$$이고$$\frac{dP}{dy^{(m)}}=\frac{dP}{dy}\frac{dy}{dy^{(m)}}=\frac{dP}{dy}\frac{1}{m}$$이므로 식을 정리하면 \(v\)는 다음과 같다.$$v=-\frac{1}{y^{(m)}}\frac{r\{1+y+ny-(1+y)^{n+1}\}-ny^{2}}{(1+y)\{r[(1+y)^{n}-1]+y\}}$$예: 만기수익률이 6%이면 다음 채권의 수정 듀레이션과 백분율 가격 변화는 어떻게 되는가?
(a) 20년 만기인 9% 만기 상환채, (b) 15년 만기인 7% 만기 상환채
답:
(a): \(m=2\), \(\displaystyle r=\frac{0.09}{2}=0.045\), \(\displaystyle y=\frac{0.06}{2}=0.03\), \(n=2\cdot20=40\)이므로 \(v=10.663\)이고 백분율 가격 변화는 다음과 같다.$$\frac{P(0.06+\Delta y^{(m)})-P(0.06)}{P(0.06)}\approx-10.663\Delta y^{(m)}$$ 그러므로 수익률이 1% 증가하면 백분율 가격 변화는 약 10.663% 감소한다.
(b): \(m=2\), \(\displaystyle r=\frac{0.07}{2}=0.035\), \(y=\frac{0.06}{2}=0.03\), \(n=2\cdot15=30\)이므로 \(v=9.502\)이고 백분율 가격 변화는 다음과 같다.$$\frac{P(0.06+\Delta y^{(m)})-P(0.06)}{P(0.06)}\approx-9.502\Delta y^{(m)}$$ 그러므로 수익률이 1% 증가하면 백분율 가격 변화는 약 9.502% 감소한다.
식$$P=100r\sum_{k=1}^{n}{(1+y)^{-k}}+100(1+y)^{-n}$$에서 때로 유용한 \(v\)에 대한 식을 유도하자.$$p_{k}=\begin{cases}r(1+y)^{-k}&\,(1\leq k\leq n-1)\\(r+1)(1+y)^{-n}&\,(k\geq n)\end{cases}$$라 하면$$P=100\sum_{k=1}^{n}{p_{k}},\,\frac{dp_{k}}{dy}=-kp_{k}(1+y)^{-1}$$이므로$$v=-\frac{1}{P}\frac{dP}{dy^{(m)}}=-\frac{1}{mP}\frac{dP}{dy}$$가 되어 다음의 식이 성립한다.$$\begin{align*}v&=\frac{1}{m(1+y)}\frac{\sum_{k=1}^{n}{kp_{k}}}{\sum_{k=1}^{n}{p_{k}}}\\&=\frac{1}{m(1+y)}\frac{\sum_{k=1}^{n}{k(1+y)^{-k}}+n(1+y)^{-n}}{r\sum_{k=1}^{n}{(1+y)^{-k}}+(1+y)^{-n}}\end{align*}$$ -만기를 고정할 때 액면 이자율이 증가하면 수정 듀레이션은 감소한다.$$\frac{dv}{dr}=-\frac{1}{m(1+y)}\frac{\sum_{k=1}^{n}{(n-k)(1+y)^{-k-n}}}{\left\{r\sum_{k=1}^{n}{(1+y)^{-k}+(1+y)^{-n}}\right\}^{2}}<0$$이므로 수정 듀레이션은 액면 이자율에 대한 감소함수이다.
액면 이자율이 높을수록, 투자는 더 빨리 상환되므로 수정 듀레이션은 더 낮아진다.
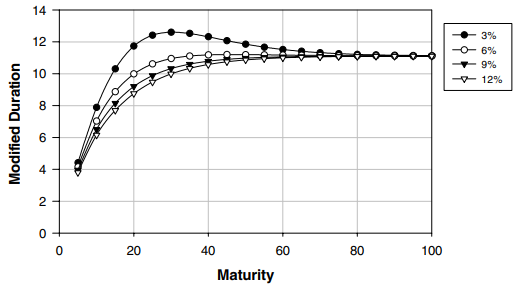
-만기를 고정할 때 수익률이 증가하면 수정 듀레이션은 감소한다.$$m\frac{dv}{dy}=-\frac{\left(\sum_{k=1}^{n}{k^{2}p_{k}}\right)\left(\sum_{k=1}^{n}{p_{k}}\right)-\left(\sum_{k=1}^{n}{kp_{k}}\right)^{2}}{(1+y)^{2}\left(\sum_{k=1}^{n}{p_{k}}\right)^{2}}-\frac{\sum_{k=1}^{n}{kp_{k}}}{(1+y)^{2}\left(\sum_{k=1}^{n}{p_{k}}\right)}$$(코시-슈바르츠 부등식) 이므로 수정 듀레이션은 수익률에 대한 감소함수이다.
수익률이 높을수록 투자는 더 빨리 상환되므로 수정 듀레이션은 더 낮아진다.
\(\displaystyle\lim_{n\,\rightarrow\,\infty}{v}=\frac{1}{ym}=\frac{1}{y^{(m)}}\)이므로 \(v\)는 수평점근선을 갖고, 이 점근선은 액면 이자율의 영향을 받지 않는다.
-수정 듀레이션은 듀레이션과 밀접하게 연관되어 있다.$$\begin{align*}v&=\frac{1}{m(1+y)}\frac{r\sum_{k=1}^{n}{k(1+y)^{-k}}+n(1+y)^{-n}}{r\sum_{k=1}^{n}{(1+y)^{-k}}+(1+y)^{-n}}\\&=\frac{1}{(1+y)m}\frac{r\sum_{k=1}^{n}{k(1+y)^{n-k}}+n}{r\sum_{k=1}^{n}{(1+y)^{n-k}}+1}\\&=\frac{1}{1+y}d\end{align*}$$이므로 \(d\)는 다음과 같다.$$d=-\frac{1}{ym}\frac{r\{1+y+ny-(1+y)^{n+1}\}-ny^{2}}{\{r[(1+y)^{n}-1]+y\}}$$ \(d=(1+y)v\)이므로 \(v\)가 \(r\)에 대해 감소함수라는 사실에서 듀레이션은 액면이자율의 감소함수이다. 왜냐하면 액면이자율이 증가하면 채권 소유자는 이자기간마다 더 많이 받게 되고, 그것이 듀레이션을 감소시키기 때문이다. 그런데 \(d=(1+y)v\)와 \(v\)가 \(y\)에 대한 감소함수라는 사실에서 \(d\)가 \(y\)에 대한 감소함수라고는 할 수 없다. 그러나 실제로 듀레이션은 수익률에 대해 감소함수이다.
듀레이션은 현금흐름을 받아들이는 데 걸리는 가중평균시간이므로, 수익률이 높아지면 현금회수가 빨라지고 따라서 듀레이션이 짧아진다.
\(d=(1+y)v\), \(\displaystyle\lim_{n\,\rightarrow\,\infty}{v}=\frac{1}{y^{(m)}}\)이므로 다음 식이 성립한다.$$\lim_{n\,\rightarrow\,\infty}{d}=\frac{1+y}{y^{(m)}}=\frac{1+\frac{y^{(m)}}{m}}{y^{(m)}}$$참고자료:
An Introduction to the Mathematics of Money Saving and Investing, Lovelock, Mendel, Wright, Springer
'확률및통계 > 기초 금융수학' 카테고리의 다른 글
| 기초 금융수학 13-주식과 주식시장 (1) | 2022.10.14 |
|---|---|
| 기초 금융수학 12-채권(4) (1) | 2022.10.13 |
| 기초 금융수학 10-채권(2) (1) | 2022.10.06 |
| 기초 금융수학 9-채권(1) (1) | 2022.10.05 |
| 기초 금융수학-8. 할부상환 (0) | 2022.10.04 |
