기초 금융수학 10-채권(2)
다음의 표는 일반적인 상황의 채권 분할 상환표이다.

위 표로부터$$\begin{align*}P_{2}&=(1+y)P_{1}-rF=(1+y)\{(1+y)P_{0}-rF\}=(1+y)^{2}P_{0}-rF\{1+(1+y)\}\\P_{3}&=(1+y)P_{2}-rF=(1+y)^{3}P_{0}-rF\{1+(1+y)+(1+y)^{2}\}\end{align*}$$이므로$$\begin{align*}P_{n}&=(1+y)P_{n-1}-rF=(1+y)^{n}P_{0}-rF\{1+(1+y)+\cdots+(1+y)^{n-1}\}\\&=(1+y)^{n}P_{0}-rF\frac{(1+y)^{n}-1}{y}\end{align*}$$이고 또한 \(\displaystyle P_{0}=\frac{P}{100}F\), \(P_{n}=F\)이므로 $$F=(1+y)^{n}\frac{P}{100}F-rF\frac{(1+y)^{n}-1}{y}$$또는$$(1+y)^{n}\frac{P}{100}=\left\{r\frac{(1+y)^{n}-1}{y}-1\right\}$$ 채권가격 \(P\)는 다음과 같다$$\begin{align*}P&=100r\sum_{k=1}^{n}{(1+y)^{-k}}+100(1+y)^{-n}\\&=100\left\{(r-y)\frac{1-(1+y)^{-n}}{y}+1\right\}\end{align*}$$1. \(P\)는 \(r\)에 대해 선형이고 \((1+y)^{n}>1\)이므로 \(\displaystyle\frac{1-(1+y)^{-n}}{y}>0\)이다. 그러므로 \(P\)는 \(r\)에 대한 증가함수이고, 따라서 액면이자율이 증가하면 가격도 증가하고 \(\displaystyle\lim_{n\,\rightarrow\,\infty}{P}=\frac{100r}{y}\)이다.
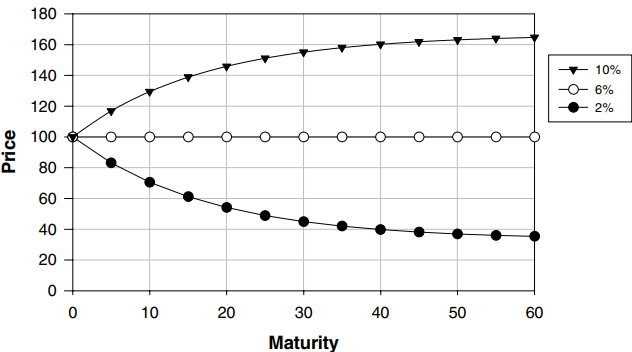
2. \(P\)를 \(n\)의 함수로 생각하면 \(P\)는 \(-100(r-y)(1+y)^{-n}\)에 대해 선형이다. 수열 \(\{-(1+y)^{-n}\}\)은 증가수열이므로 \(P\)도 \(r>y\)이면 \(n\)에 대해 증가함수이고 \(r<y\)이면 \(n\)에 대한 감소함수이다. 또한 \(\displaystyle\lim_{n\,\rightarrow\,\infty}{P}=\frac{100r}{y}\)도 성립한다.
3. \(P\)를 \(y\)의 함수로 생각하자.$$\frac{\partial P}{\partial y}=-100r\sum_{k=1}^{n}{k(1+y)^{-k-1}}-100n(1+y)^{-n-1}<0$$이므로 \(P\)는 \(y\)에 대한 감소함수이고 \(y^{(m)}=my\)이므로 따라서 \(y^{(m)}\)의 감소함수이다.
그러므로 수익률이 오르면 가격은 떨어지고 수익률이 떨어지면 가격은 오른다. 따라서 흔히 인용하는 만기상환채의 다음 성질이 성립한다.
정리 7.3(가격 및 수익률 정리) 만기 상환채의 가격과 수익률은 반대로 움직인다.$$\frac{\partial^{2}P}{\partial y^{2}}=100r\sum_{k=1}^{n}{k(k+1)((1+y)^{-k-2}}+100n(n+1)(1+y)^{-n-2}>0$$이므로 \(y\)에 대한 \(P\)의 그래프는 위로 오목하다.$$\lim_{y\,\rightarrow\,\infty}{P}=0,\,\lim_{y\,\rightarrow\,0+}{P}=100nr+100$$이므로 \(y\geq0\)인 \(y\)에 대해 다음의 부등식을 만족해야 한다.$$0<P<100nr+100$$정리 7.4(수익률 존재 정리) \(P\)가 부등식 \(0<P<100nr+100\)을 만족하면 식$$\frac{P}{100}(1+y)^{n}=r\sum_{k=1}^{n}{(1+y)^{k-1}}$$은 \(P,\,r,\,n\)에 대해 해 \(y\)를 갖는다.
채권가격식 \(P\)를 \(y\)에 대한 식$$y=r\frac{(P-100)y}{100\{1-(1+y)^{-n}\}}$$으로 나타낼 수 있고, \(y=0\)근방에서 유효한 근사식$$(1+y)^{-n}\approx 1-ny+\frac{n(n+1)}{2}y^{2}$$를 이용하면$$1-(1+y)^{-n}\approx n\left(y-\frac{n+1}{2}y^{2}\right)$$이고 또한$$\frac{1}{1-\frac{n+1}{2}y}\approx1+\frac{n+1}{2}y$$이므로 다음의 근사식이 성립한다.$$\begin{align*}y&=r-\frac{(P-100)y}{100\{1-(1+y)^{-n}\}}\approx r-\frac{P-100}{100n\left\{1-\frac{n+1}{2}y\right\}}\\&\approx r-\frac{P-100}{100n}\left(1+\frac{n+1}{2}y\right)\end{align*}$$ 이 식을 \(y\)에 대해 풀면$$(1)\,y\approx\frac{100nr+100-P}{P\frac{n+1}{2}+100\frac{n-1}{2}}$$이고 이때 \(n\)이 크면$$(2)\,y\approx\frac{\frac{100-P}{n}+100r}{\frac{P+100}{2}}$$가 되는데 이것을 다음과 같이 볼 수 있다.$$y\approx\frac{\text{기간당 가격변화의 평균}+\text{액면이자}}{\text{가격과 액면가의 평균}}$$ 이때 식 (1), (2)를 \(y\)를 구하기 위한 뉴턴 방법의 초기 추정치로 사용할 수 있다.
예: 20년 만기이고 액면가 1,000달러인 9% 만기 상환채의 가격이 77.43달러이면 만기수익률은?
답:$$P=100(r-y)\frac{1-(1+y)^{-n}}{y}+100$$이고 \(P=77.43\), \(r=\frac{0.09}{2}=0.045\), \(n=40\)이므로 다음의 방정식을 풀어야 한다.$$77.43=100(0.045-y)\frac{1-(1+y)^{-40}}{y}+100$$ 근삿값$$y\approx\frac{100nr+100-P}{\frac{n+1}{2}P+\frac{n-1}{2}100}=0.0573,\,y\approx\frac{\frac{100-P}{n}+100r}{\frac{P+100}{2}}-=0.0571$$을 뉴턴 방법의 초기값으로 사용하면 \(y=0.06\)이고 따라서 수익률은 \(y^{(m)}=0.12(12\text{%})\)이다.
지금까지는 이자 지급일의 채권 가격을 계산했다. 이제 실제로 자주 생기는 경우인 이자기간 도중에 채권이 매매되는 경우를 보자. 구매자 입장에서 다음 이자가 구매자에게는 첫 이자이고 \(n\)번의 이자 지급기간이 남았다고 하자. 채권가격이 계산되는 시점에 남은 첫 이자 지급기간의 비율을 \(w(0<w<1)\)라 하자. 해결해야 할 문제가 두 가지 있다.
1. 첫 이자의 일부(이자 지급기간의 \(1-w\))는 판매자에게, 일부(이자 지급기간의 \(w\))는 구매자에게 속한다.
2. 구매자가 첫 이자를 전부 받을 것이므로 판매자는 자신이 소유했던 시간에 비례하여, 즉 경과이자(accrued interest)라 부르는, 이자의 일부 \((1-w)rF\)를 받아야 한다.

시간 \(1-w\)를 현재 시각으로 사용하면 다음과 같이 됨을 알 수 있다.$$\frac{P}{100}F=rF\left\{\frac{1}{(1+y)^{w}}+\frac{1}{(1+y)^{1+w}}+\cdots+\frac{1}{(1+y)^{n-1+w}}\right\}+\frac{F}{(1+y)^{n-1+w}}$$이를 다음과 같이 나타낼 수 있고$$\begin{align*}\frac{P}{100}&=\frac{r}{(1+y)^{w}}\left\{1+\frac{1}{(1+y)}+\cdots+\frac{1}{(1+y)^{n-1}}\right\}+\frac{1}{(1+y)^{n-1+w}}\\&=\frac{r}{(1+y)^{w}}\frac{\left(\frac{1}{1+y}\right)^{n}-1}{\frac{1}{1+y}-1}+\frac{1}{(1+y)^{n-1+w}}\end{align*}$$이것을 \(P\)에 대해 나타내면 다음과 같다.$$\begin{align*}P&=\frac{100r}{(1+y)^{w}}\left\{\frac{1+y-(1+y)^{1-n}}{y}\right\}+\frac{100}{(1+y)^{n-1+w}}\\&=100\left\{(r-y)\frac{1-(1+y)^{-n}}{y}+1\right\}(1+y)^{1-w}\end{align*}$$ 채권가격으로 지불해야 하는 금액은 \(P\)에 경과이자를 합한 액수이다.
서로 다른 두 채권을 비교해야 하는데 \(P\)는 \(r,\,y,\,n\)의 함수여서 비교가 어렵다. 그러나 위험이라는 측면에서 두 채권을 비교할 수 있다.
Q: 10년 무이표 채권과 10년 만기 상환채 이 둘 다 수익률이 7%일 때 어떤 채권이 더 위험한가?
A: 채무불이행시 두 번째는 이자를 얼마라도 받을 수 있으므로 두 번째가 덜 위험하다.
\(n\)개의 추 \(a_{1},\,...,\,a_{n}\)이 같은 간격 \(S\)를 사이에 두고 무게가 없는 널판 위에 있다고 하자. 이 추들이 평형을 이루는 거리 \(d\)를 찾자.

\(d\)가 \(ks\)와 \((k+1)s\)사이에 있으면 \(d\)의 왼쪽에 있는 추가 오른쪽에 있는 것과 균형을 이루어야 하므로 다음의 식이 성립해야 한다.$$(d-s)a_{1}+\cdots+(d-ks)a_{k}=\{(k+1)s-d\}a_{k+1}+\cdots(ns-d)a_{n}$$ 이를 \(d\)에 대해 풀면$$\begin{align*}d&=\frac{sa_{1}+2sa_{2}+\cdots+nsa_{n}}{a_{1}+a_{2}+\cdots+a_{n}}\\&=s\frac{\sum_{k=1}^{n}{ka_{k}}}{\sum_{k=1}^{n}{a_{k}}}\end{align*}$$이고, 이것을 \(a_{1},\,a_{a},\,...,\,a_{n}\)의 가중평균(weighted average)이라고 한다.
이 아이디어를 1년에 \(m\)번 지급되는 이자의 미래가에 주시해 채권에 적용한다.

이 경우 \(\displaystyle s=\frac{1}{m}\), \(k=1,\,...,\,n-1\)에 대해 \(a_{k}=rF(1+y)^{n-k}\), \(a_{n}=rF+F\)이므로 \(d\)는 다음과 같다.$$\begin{align*}d&=\frac{1}{m}\times\frac{\sum_{k=1}^{n-1}{krF(1+y)^{n-k}}+n(rF+F)}{\sum_{k=1}^{n}{rF(1+y)^{n-k}}+rF+F}\\&=\frac{1}{m}\times\frac{r\sum_{k=1}^{n}{k(1+y)^{n-k}}+n}{r\sum_{k=1}^{n}{(1+y)^{n-k}}+1}\end{align*}$$ 이 \(d\)를 존속기간을 뜻하는 듀레이션(duration)이라고 한다. 듀레이션의 단위는 시간이고 모든 현금흐름을 받는 데 걸리는 시간의 가중평균이다. 그러므로 같은 수익률인 채권에 대해 듀레이션이 짧을수록 위험은 더 낮다.
예: 만기수익률이 6%일 때 (a) 20년 만기의 9% 만기상환채, (b) 15년 만기의 7% 만기상환채
(a): \(m=2\), \(\displaystyle r=\frac{0.09}{2}=0.045\), \(\displaystyle y=\frac{0.06}{2}=0.03\), \(n=40\)이므로 듀레이션 공식에 의해 \(d=10.983\)년 이다.
(b): \(,=2\), \(\displaystyle r=\frac{0.07}{2}=0.035\), \(\displaystyle y=\frac{0.06}{2}=0.03\), \(n=30\)이므로 듀레이션 공식에 의해 \(d=9.787\)년 이다.
따라서 두 번째 채권 (b)가 덜 위험하다.
듀레이션 개념을 모든 현금흐름으로 확장할 수 있다. \(C_{k}\)가 주기가 \(k(0\leq k\leq n)\)이고 연간 \(m\)회 지급되는 현금흐름이면 현금흐름은 다음과 같다.
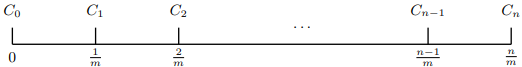
주기당 이자율이 \(y\)일 때, 이 현금흐름의 듀레이션 \(d\)는 이 현금흐름의 미래가의 시간 가중평균이다. 즉, 다음과 같다.$$d=\frac{\sum_{k=0}^{n}{\frac{k}{m}C_{k}(1+y)^{n-k}}}{\sum_{k=0}^{n}{C_{k}(1+y)^{n-k}}}=\frac{\sum_{k=0}^{n}{kC_{k}(1+y)^{n-k}}}{m\sum_{k=0}^{n}{C_{k}(1+y)^{n-k}}}$$참고자료:
An Introduction to the Mathematics of Money Saving and Investing, Lovelock, Mendel, Wright, Springer
'확률및통계 > 기초 금융수학' 카테고리의 다른 글
| 기초 금융수학 12-채권(4) (1) | 2022.10.13 |
|---|---|
| 기초 금융수학 11-채권(3) (1) | 2022.10.07 |
| 기초 금융수학 9-채권(1) (1) | 2022.10.05 |
| 기초 금융수학-8. 할부상환 (0) | 2022.10.04 |
| 기초 금융수학-7. 대출과 위험 (0) | 2022.10.04 |
