기초 금융수학-6. 연금
연금:
주기(정기적인 시간)마다 지급되는 일정 금액
기말급 연금(ordinary annuity):
지급이 주기의 말에 시행되는 연금
기시급 연금(annuity due):
지급이 주기가 시작될 때 시행되는 연금
기말급 연금
\(P\): 매 주기 말에 투자하는 금액
\(n\): 전체 주기 수(total number of periods)
\(P_{n}\): \(n\)째 주기 말의 연금의 미래가
\(m\): 연간 이자 주기 수(number of interest periods per year)
\(i^{(m)}\): 소수로 표기한 명목 이자율(연간 이자율, annual interest rate)
\(i\): 이자주기당 이자율(interest rate per interest period) \(\displaystyle i=\frac{i^{(m)}}{m}\)
정리 4.1(기말급 연금의 미래가 정리) 매 주기 말에 \(P\)를 \(n\)주기 동안 투자하면, 1년에 \(m\)번 주기가 있고 명목이율이 \(i^{(m)}\)일 때, \(n\)번째 주기 후에 연금의 미래가 \(P_{n}\)은 다음과 같다.$$P_{n}=\sum_{k=1}^{n}{P(1+i)^{k-1}}=P\frac{(1+i)^{n}-1}{i}$$증명: 수학적 귀납법 또는 재귀관계를 이용한다.$$*1+x+x^{2}+\cdots+x^{n-1}=\frac{x^{n}-1}{x-1}\,(x\neq1)$$이 상황을 다음과 같이 나타낼 수 있다.

첫 지급금 \(P\)의 \(n\)번 주기 후 미래가는 \(P(1+i)^{n-1}\), 둘째 지급금 \(P\)의 미래가는 \(P(1+i)^{n-2}\),...이므로 식$$P_{n}=P(1+i)^{n-1}+P(1+i)^{n-2}+\cdots+P(1+i)+P$$는 위 그림과 일치한다.
예: 스미스 부부는 20세 딸에게 장기간에 거친 생일선물을 주기로 했다.
이 부부는 딸의 명의로 명목이자율 8%로 2,000달러를 다음 5번의 생일에 저축하고, 그다음에는 해마다 적립하지 않기로 했다. 이 부부의 딸이 65세가 되었을 때의 금액은?
답: \(n=5\)이고, 5년 후 딸은$$P_{5}=2000\frac{(1+0.08)^{5}-1}{0.08}=11,733.20\$ $$을 갖게 된다. 이제 이 금액이 40년 동안 8%로 투자되어 \(11733.20(1+0.08)^{40}=254,898.16\$\)이 된다.
\(P_{n}\)의 현재가는 \(P_{0}\)이고 이때 \(P_{n}=P_{0}(1+i)^{n}\)이므로 기말급 금의 현재가는$$P_{0}=P_{n}(1+i)^{-n}=P\frac{(1+i)^{n}-1}{i}(1+i)^{-n}=P\frac{1-(1+i)^{-n}}{i}$$이다. 그러므로 다음 정리가 성립한다.
정리 4.2(기말급 연금의 현재가 정리) (1년에 \(m\)번의 주기가 있을 때) \(n\)번의 주기 말에 금액 \(P\)를 명목이율 \(i^{(m)}\)으로 투자하면, 이 연금의 현재가 \(P_{0}\)는 \(\displaystyle i=\frac{i^{(m)}}{m}\)일 때 다음과 같다.$$P_{0}=\frac{P_{n}}{(1+i)^{n}}=\sum_{k=1}^{n}{\frac{P}{(1+i)^{n+1-k}}}=P\frac{1-(1+i)^{-n}}{i}$$ 위 식을 다음과 같이 나타낼 수 있다.

이 것을 처음에 대출 \(P_{0}\)를 받고 \(P\)를 \(n\)번의 지급주기에 걸쳐 상환하는 것(대출을 할부상환 한다고 한다)으로 해석할 수 있다. 다르게 말하자면 "\(n\)달 동안 \(P\)를 갚아갈 수 있다면, 월 이자율 \(i\)로 얼마나 많이 빌릴 수 있는가?"에 답할 수 있다. 그러나 일반적으로 "\(P_{0}\)를 월 이자율 \(i\)로 빌려서 한달에 \(P\)씩 갚는다면 대출을 상환하는데 얼마나 걸리는가?"에는 답할 수 없는데 식 \(\displaystyle P_{0}=P\frac{1-(1+i)^{-n}}{i}\)를 \(n\)에 대해 풀면$$n=\frac{\displaystyle\ln\left(\frac{P}{P-iP_{0}}\right)}{\ln(1+i)}$$이 되는데 좌변은 정수이나 우변은 일반적으로 정수는 아니다.
예: 앤더슨 가족은 할부로 새 주택을 구입하는 것을 고려하고 있다. 그들은 30년 동안 한 달에 700달러 씩 지출할 수 있다. 현재 이자율이 8%라면 얼마를 대출할 수 있는가?
답: \(P=700\), \(m=12\), \(\displaystyle i=\frac{0.08}{12}\), \(n=30\times12=360\)이므로$$P_{0}=700\frac{\displaystyle1-\left(1+\frac{0.08}{12}\right)^{-360}}{\displaystyle\frac{0.08}{12}}=95,398.45\$ $$이고, 약 95,000달러를 대출받을 수 있다.
감채기금(sinking fund):
미래의 \(n\)번째 주기에 해당하는 특정 날짜에 목표액 \(F\)가 적립될 것을 목표로 이자율 \(i^{(m)}\)으로 일정한 금액 \(P\)를 1년에 \(m\)번 (보통 매월) 정기적으로 예치하는 계좌
마지막 주기를 포함하여 각 주기 말에 예치된다면 시간도표는 다음과 같다.
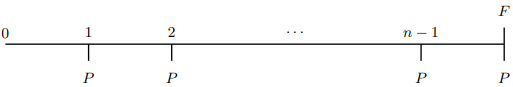
이 것은 기말급 연금에 해당하므로 \(\displaystyle i=\frac{i^{(m)}}{m}\)이라 하면 \(\displaystyle F=P\frac{(1+i)^{n}-1}{i}\)이다.
보통 감채기금은 "특정한 시점에 최종 목표금액에 도달하려면 매 주기에 얼마나 많이 적립해야 하는가?"와 같은 질문이 발생한다. 이것은 \(P\)를 \(F\), \(n\), \(i\)의 항으로 표현하는 것과 같고 \(\displaystyle P=F\frac{i}{(1+i)^{n}-1}\)로 나타낼 수 있다.
예: 리처드는 5년 안에 승용차를 구입할 계획이 있다. 그는 20,000달러가 필요할 것으로 보고 있다. 차를 교체하려면 명목이율 6%인 월 복리 감채기금에 매월 얼마나 넣어야 하는가?
답: \(F=20000\), \(n=5\times12=60\), \(\displaystyle i=\frac{0.06}{12}=0.005\)이므로$$P=20000\frac{0.005}{(1+0.005)^{60}-1}=286.656$$즉 월 286.66달러이다.
정리 4.3 감채기금에 대한 주기적인 지급액 \(\displaystyle P=F\frac{i}{(1+i)^{n}-1}\)는 \(n(>1)\)일에 대하여 다음의 부등식을 만족해야 한다.$$\frac{F}{n}(1+i)^{-n}<P<\frac{F}{n}$$기시급 연금
\(P\): 매 기간 초에 투자하는 금액(amount)
\(n\): 전체 기간 수(total number of periods)
\(P_{n}\): 연금의 \(n\)째 이자기간 말의 미래가
\(m\): 연간 기간 수(number of periods per year)
\(i^{(m)}\): 소수로 표기한 명목이자율
\(i\): 이자기간당 이자율(interest rate per interest period), \(\displaystyle i=\frac{i^{(m)}}{m}\)
다음은 기시급 연금의 일반적인 시간도표이다.

정리 4.4(기시급 연금의 미래가 정리) \(n\)번의 기간(1년에 \(m\)번의 기간이 있다고 가정)동안 매 기간 초에 \(P\)를 명목이율 \(i^{(m)}\)으로 투자하면 \(n\)번의 기간 후 연금의 미래가 \(P_{n}\)은 다음과 같다.$$P_{n}=\sum_{k=1}^{n}{P(1+i)(1+i)^{k-1}}=P(1+i)\frac{(1+i)^{n}-1}{i}$$*참고$$1+x+x^{2}+\cdots+x^{n-1}=\frac{x^{n}-1}{x-1}\,(x\neq1)$$ \(P_{n}\)의 현재가는 \(P_{0}\)로 \(P_{n}=P_{0}(1+i)^{n}\)이다. 여기서 다음 정리를 얻을 수 있다.
정리 4.5(기시급 연금의 현재가 정리) \(n\)번의 기간(1년에 \(m\)번의 기간이 있다고 가정) 동안 매 기간 초에 \(P\)를 명목이율 \(i^{(m)}\)으로 투자하면 연금의 현재가 \(P_{0}\)는 다음과 같다.$$P_{0}=\frac{P_{n}}{(1+i)^{n}}=P(1+i)\frac{1-(1+i)^{-n}}{i}$$영구연금(perpetuity):
영원히 지속되는 연금(금융기관이 폐업하지 않는다는 가정 하에서)
정리 4.6 지급 주기 당 이자율 \(i\)로 지급주기당 금액 \(P\)를 지급하는 영구연금의 현재가 \(P_{0}\)는 다음과 같다.$$P_{0}=\frac{P}{i}$$증명:$$P_{0}=P(1+i)^{-1}+P(1+i)^{-2}+\cdots=P(1+i)^{-1}\frac{1}{\displaystyle 1-\frac{1}{1+i}}=\frac{P}{i}$$참고자료:
An Introduction to the Mathematics of Money Saving and Investing, Lovelock, Mendel, Wright, Springer
'확률및통계 > 기초 금융수학' 카테고리의 다른 글
| 기초 금융수학-8. 할부상환 (0) | 2022.10.04 |
|---|---|
| 기초 금융수학-7. 대출과 위험 (0) | 2022.10.04 |
| 기초 금융수학-5. 인플레이션 세금 (1) | 2022.10.03 |
| 기초 금융수학-4. 복리(3) (0) | 2022.10.02 |
| 기초 금융수학-3. 복리(2) (0) | 2022.10.01 |
