기초 금융수학-5. 인플레이션 세금
인플레이션과 세금은 투자의 실효이자율(EFF)을 감소시키는 요인이다.
인플레이션(물가상승):
한 국가의 재화와 용역 가격 등의 전반적인 물가가 지속적으로 상승하는 경제상태. 이자처럼 작용하나 반대방향으로 움직인다.
예: 어느 해에 인플레이션이 10%이면 연초에 100달러 가치인 상품이 연말에는 110달러의 가치가 되어 그 상품을 연초에 비해 \(\displaystyle\frac{100}{110}\)개의 상품만 구매할 수 있다.
따라서 연간 인플레이션율이 \(i_{\text{inf}}\)이면, 연초의 \(P_{0}\)는 연말에 \(\displaystyle\frac{P_{0}}{1+i_{\text{inf}}}\)의 구매력이 된다.
정리 3.1(구매력 정리) 연간 인플레이션율이 \(i_{\text{inf}}\)로 일정하면, \(n\)년 후 구매력은 다음과 같이 감소한다.$$P_{n}=\frac{P_{0}}{(1+i_{\text{inf}})^{n}}$$-\(i_{\text{inf}}>0\)이면, \(\{P_{n}\}\)은 \(\displaystyle\lim_{n\,\rightarrow,\,\infty}{P_{n}}=0\)인 감소수열이다. 이것은 인플레이션 기간 동안 시간이 지남에 따라 화폐가 구매할 수 있는 물건은 점점 더 적어짐을 뜻한다.
-디플레이션(물가하락)은 인플레이션과 반대이고 \(i_{\text{inf}}<0\)이다. 이때 \(\{P_{n}\}\)은 \(\displaystyle\lim_{n\,\rightarrow,\,\infty}{P_{n}}=0\)인 증가수열이다. 이것은 디플레이션 기간 동안 시간이 지남에 따라 화폐가 구매할 수 있는 물건은 점점 더 많아짐을 뜻한다.
예: 케이트는 영화 표를 7달러에 구입했다. 인플레이션율이 5%로 지속된다면 20년 후에 오늘의 금액으로 얼마나 지불해야 하는가?
답: \(P_{20}=7\)일 때 \(P_{0}\)가 오늘의 금액으로 지불해야 하는 금액이다. \(P_{n}=P_{0}(1+i_{\text{inf}})^{-n}\)에서 \(P_{0}=7(1+0.05)^{20}=18.57\)이 된다. 그러므로 인플레이션으로 인한 20년 후 영화 표의 가격은 18.57달러이다.
\(P_{0}\)를 실효 이자율 \(i_{\text{ieff}}\)인 계좌에 입금했다고 하자. 인플레이션율 \(i_{\text{inf}}\)가 일정하다면 \(n\)년 후에 계좌에 있는 금액의 구매력은 다음과 같다.$$P_{n}=P_{0}(1+i_{\text{eff}})^{n}\left(\frac{1}{1+i_{\text{inf}}}\right)^{n}=P_{0}\left(\frac{1+i_{\text{eff}}}{1+i_{\text{inf}}}\right)^{n}$$실 이자율(real rate of interest):
인플레이션을 따라 조정한 이율 \(i_{\text{eff}}\)로 \(P_{0}\)가 이에 따라 연 단위 복리로 이자계산될 때 \(P_{n}\)으로 증가하게 되는 연이율 실 이자율 \(i_{\text{real}}\)을 도입하면 \(P_{n}=P_{0}(1+i_{\text{real}})^{n}\)이고 앞의 식으로부터$$1+i_{\text{real}}=\frac{1+i_{\text{eff}}}{1+i_{\text{inf}}}$$이므로$$i_{\text{real}}=\frac{1+i_{\text{eff}}}{1+i_{\text{inf}}}-1=\frac{i_{\text{eff}}-i_{\text{inf}}}{1+i_{\text{inf}}}$$이고, 이것을 \(i_{\text{eff}}\)에 대해 풀면 다음과 같이 된다.$$i_{\text{eff}}=i_{\text{inf}}+i_{\text{real}}+i_{\text{inf}}i_{\text{real}}$$소비자 물가지수(consumer price index, CPI):
일상생활을 위해 소비자가 구입하는 재화와 용역의 시간에 대한 평균가격을 나타내는 지표.
*미국의 소비자 물가지수는 가장 일반적이고 포괄적인 지수이며 '인플레이션율'의 근원으로 인용된다.
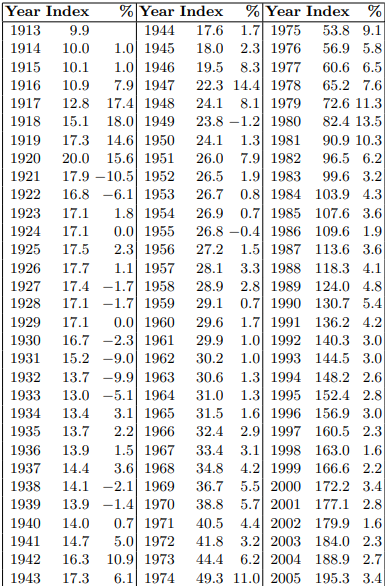
예: 2004년의 지수가 188.9, 2005년의 지수가 195.3이면 2005년의 인플레이션율은 다음과 같다.$$\frac{2005년 지수-2004년 지수}{2004년 지수}=\frac{195.3-188.9}{188.9}=0.0339\approx0.034(3.4\text{%})$$예: 1970년 지수는 38.8, 2005년 지수는 195.3이다. 이것은 1970년에 가격이 38.80달러인 상품이 2005년에는 195.30달러가 되었음을 뜻한다. 그러므로 35년 후 금액 \(P_{0}\)의 구매력은 \(\displaystyle P_{35}=\frac{38.8}{195.3}P_{0}\)로 감소하고 따라서 인플레이션율 \(i_{\text{inf}}\)는 \(\displaystyle\frac{38.8}{195.3}P_{0}=P_{0}\left(\frac{1}{1+i_{\text{inf}}}\right)^{35}\), 즉 다음과 같다.$$i_{\text{inf}}=\left(\frac{38.8}{195.3}\right)^{\frac{1}{35}}-1=0.047\approx0.05(5%)$$ 금액 \(P_{0}\)를 이자가 붙는 계좌에 실효이자율 \(i_{\text{eff}}\)로 예치하면, 1년 후 \(P_{0}(1+i_{\text{eff}})\)가 될 것이다. 그러므로 그 해의 세전 이자는 \(i_{\text{eff}}P_{0}\)이다. 이 이자에는 세금이 포함되어서 세율이 \(t\)일 때 \(i_{\text{eff}}P_{0}t\)를 세금으로 납부해야 하고, 둘째 해에 재투자 가능한 실제 세후 금액은 다음과 같다.$$P_{1}=P_{0}(1+i_{\text{eff}})-i_{\text{eff}}P_{0}t=P_{0}\{1+(1-t)i_{\text{eff}}\}$$ 1년 후 이 금액은 세전 \(P_{1}(1+i_{\text{eff}})\)이므로 세후에는 다음과 같다.$$P_{2}=P_{1}(1+i_{\text{eff}})-i_{\text{eff}}P_{1}t=P_{1}\{1+(1-t)i_{\text{eff}}\}$$정리 3.3(세금 정리) 연간 실효이자율이 \(i_{\text{eff}}\), 연간 세율이 \(t\)이면, \(n\)년 후 \(P_{0}\)의 세후 미래가는 다음과 같다.$$P_{n}=P_{0}\{1+(1-t)i_{\text{eff}}\}^{n}$$ 세후이자율(after-tax rate of interest) \(i_{\text{tax}}\)를 도입해 이 이율로 복리로 이자계산될 때 \(P_{0}\)가 세후에 \(P_{n}\)이 되게 하자. 그러면 \(P_{n}=P_{0}(1+i_{\text{tax}})^{n}\)이고 세금정리에 의해 \(i_{\text{tax}}=(1-t)i_{\text{eff}}\)이다.
참고자료:
An Introduction to the Mathematics of Money Saving and Investing, Lovelock, Mendel, Wright, Springer
'확률및통계 > 기초 금융수학' 카테고리의 다른 글
| 기초 금융수학-7. 대출과 위험 (0) | 2022.10.04 |
|---|---|
| 기초 금융수학-6. 연금 (1) | 2022.10.03 |
| 기초 금융수학-4. 복리(3) (0) | 2022.10.02 |
| 기초 금융수학-3. 복리(2) (0) | 2022.10.01 |
| 기초 금융수학-2. 복리(1) (0) | 2022.10.01 |
