수학사 19-페르가의 아폴로니우스(1)
1. 잃어버린 저작
헬레니즘 시대의 초기 한 두 세기 동안 그 시대를 포함하여 이전이나 이후의 수학자 대부분은 훨씬 뛰어넘는 훌륭한 수학자 세 사람이 나왔다. 그들은 유클리드, 아르키메데스, 아폴로니우스이고, 기원전 300~200년을 그리스 수학의 '황금시대'라고 하는 것도 그들의 업적이다. 그러나 수학의 발달은 예술과 문학보다 조금 늦었다. 그것은 더욱 넓은 의미에서 '그리스의 황금시대'란 기원전 5세기 중엽의 '페리클레스 시대'를 가리키기 때문이다.
헬레니즘 시대 전체에 걸쳐 알렉산드리아는 서구 세계에서 수학의 중심지였고, 아폴로니우스는 팜필리아(소아시아 남부)의 페르가에서 태어났다. 그러나 알렉산드리아에서 교육을 받고, 그곳의 대학에서 잠깐 가르쳤고, 알렉산드리아 다음으로 큰 페르가뭄에 잠시 있던 적도 있다.
아폴로니우스는 기본수를 100만으로 하고, 그 거듭제곱을 사용하 '네 수'의 체계를 만들었다. 이 수 체계는 파푸스의 '수학집성' 2권 중 남은 부분의 마지막에 있다. 여기서 \(5,462,360,064\times10^{6}\)은 \(\mu^{\gamma},\epsilon\nu\xi\beta\cdot\mu^{\beta},\gamma\chi\mu^{\alpha},\zeta\nu\)로 쓰였고, \(\mu^{\gamma}\), \(\mu^{\beta}\), \(\mu^{\alpha}\)는 각각 1만의 세제곱, 제곱, 1제곱이다.
아폴로니우스는 '빠른 계산법'(지금은 전해지지 않는다)을 통해 아르키메데스보다 정확히 \(\pi\)의 근삿값(현재 알려진 \(3.1416...\))을 계산했는데 이 값은 뒤의 톨레미 시대와 인도에서도 나오나 어떻게 얻었는지는 알 수 없다.
아폴로니우스는 '비례 절단', '면적 절단', '정량 절단', '접촉', '기울기', '평면의 자취'등의 저작을 남겼으나 현재는 전해지지 않는다. 위 저작 6권은 유클리드의 수를 놓은 높은 두 편(지금은 전해지지 않는다)과 함께 파푸스의 '분석론 보전'이라는 논문집에 정리되어있다. 이 '보전'은 오늘날의 '해석기하학'의 색채가 강한 것이었다. 고대에 유클리드보다 아폴로니우스가 위대한 기하학자로 알려진 데에는 그 나름의 까닭이 있다.
2. 잃어버린 저작의 복원
17세기는 잃어버린 기하학 책을 복원하려는 경쟁이 가장 활발한 시대였고, 아폴로니우스의 논문 몇 가지가 복원되었다. 그 중 '평면의 자취'에서 다음의 두 자취가 거론되었다.
(1) 두 정점에서 거리의 제곱의 차가 일정한 점의 자취는 두 점을 잇는 직선에 수직인 직선이다.
(2) 두 점에서 거리의 비가 일정(1이 아닌)한 점의 자취는 원이다(아폴로니우스의 원으로 알려져 있다).
(2)의 원은 이미 아리스토텔레스가 알고 있었고, 무지개의 반원형을 수학적으로 증명하는데 사용했다. '비례 절단'은 일반적인 문제 하나를 여러 경우에 적용하여 다루었다. 그 문제는 '두 직선과 그 위에 정점이 하나씩 있고, 주어진 세 번째 점을 지나는 직선 하나를 그을 때 그것이 각 직선을 잘라낸 (두 직선 위의 각 정점에서 교점까지의) 선분의 비를 주어진 비가 되도록 하는 것'이다. 이 문제는 \(ax-x^{2}=bc\)골의 이차방정식을 푸는 것, 곧 어떤 선분 위에 있는 직사각형에 정사각형만큼 모자라는 직사각형을 적용시킨 것과 같다.

한편 '면적 절단'의 문제는 잘라낸 선분을 주어진 비가 되는 것이 아니라 잘라낸 선분의 곱이 주어진 직사각형이 되게 하는 것을 제외하면 실상 위 문제와 같다. 이때 여기서는 \(ax+x^{2}=bc\)꼴의 이차방정식이 등장한다.
다음의 정량절단은 1차원 해석기하학이라고도 할 수 있는 내용이다. 거기서는 기하학의 형식을 취한 전통적인 그리스적 대수 해석법을 사용하여 다음과 같은 일반적인 문제를 고찰하고 있다.
직선 위에 네 점 \(A,\,B,\,C,\,D\)가 주어질 때 같은 직선 위의 다섯번째 점 \(P\)를 \(AP\)와 \(CP\)가 만드는 직사각형과 \(BP\)와 \(DP\)가 만드는 직사각형이 주어진 비(\(AP\cdot CP=\lambda BP\cdot DP\))가 되도록 결정하라는 문제이다.
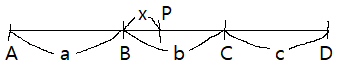
이 문제도 또한 이차방정식의 해를 구하는 문제로 만들 수 있다. 아폴로니우스는 그 밖의 경우와 마찬가지로, 이 문제도 해가 속하는 가능한 범위와 해의 개수를 포함하여 철저히 연구했다.
3. 아폴로니우스 문제
'접촉'에 있는 논문은 '아폴로니우스의 문제'로 널리 알려져 있다. 이는 점, 선, 원 가운데 아무렇게나 고른 세 개의 요소 모두에 접하는 원을 그리는 문제이다.
이 문제는 10가지 경우가 있는데 가장 쉬운 두 경우인 세 점 또는 세 직선에 접하는 원을 그리는 것에서 가장 어려운 경우인 세 원에 접하는 원을 그리는 것까지 있다.
아폴로니우스의 풀이법 자체는 전해지지 않지만 파푸스가 남긴 정보로 다시 보일 수 있다. 그럼에도 일반적으로 16, 17세기 학자들은 아폴로니우스가 마지막 세 원의 경우는 풀지 못했다고 생각해 이 문제를 자신의 능력에 대한 도전으로 간주했다. 곧은 자와 컴파스로만 이 문제를 푼 사람에는 뉴턴이 있다.
아르키메데스에 의한 각의 삼등분법은 주어진 점을 지나고 기울기가 자유로이 바뀌는 직선(\(SP\))을 따라 주어진 길이\((ST)\)를 직선과 원 사이에 놓는 방법인데, 그것은 노이시스(neusis, 기울기)로 푸는 전형적인 예이다. 한편 아폴로니우스의 기울기는 '평면'의 방법, 곧 컴파스와 곧은 자만 쓰는 방법으로 푸는 노이시스 문제를 고찰했다. 파푸스에 따르면 '기울기'에서 다룬 문제는 주어진 원 안에서 정점을 지나도록 하며, 기울기가 있는 주어진 길이의 현을 끼운다는 내용이었다.
아폴로니우스는 '십이면체와 이십면체의 비교'에서 같은 구에 내접하는 정십이면체와 정이십면체의 오각형과 삼각형의 면은 각각 구의 중심에서 같은 거리에 있다는 정리를 증명했다.
4. 원과 주전원
아폴로니우스는 천문학자이기도 했다. 에우독소스는 중심이 같은 구(동심구)를 사용했는데, 아포롤니우스는 다른 두 체계, 곧 주전원 운동계와 이심원 운동계를 제창했다.

주전원 체계에서는 행성 \(P\)가 작은 원(주전원)의 둘레를 일정하게 움직인다고 가정하고, 그 원의 중심 \(C\)는 그것에 대응하여 지구 \(E\)를 중심으로 하는 큰 원(종원) 위를 일정하게 움직인다고 생각한다.
이심원 체계에서는 행성 \(P\)는 대원 위를 일정하게 움직이고, 대원의 중심 \(C'\)은 그것에 대응하며 \(E\)를 중심으로 하는 작은 원 위를 움직인다. \(PC=C'E\)라 하면 두 기하학적 체계는 동치이다.
이 원과 주전원 또는 이심원 이론은 톨레미(알렉산드리아)의 저작을 통해 상세한 정밀감과 예측가능한 정확함을 필요로 하는 수리천문학자들에게 받아들여졌다.
5. 원뿔곡선
아폴로니우스는 학자로서 많은 글을 썼지만 겨우 두 편의 글만 본래 그대로 남아있다. 그 중 '비례 절단'의 그리스어 판은 없어졌고, 아라비아어, 라틴어를 거쳐 여러나라 언어로 출판되었다.
아폴로니우스의 저작에서 많은 부분이 그대로 남을 수 있던 것은 '원뿔곡선'뿐이고, 이것은 그의 최고 걸작으로 유클리드의 '원론'과 맞먹는 수준이다.
원뿔곡선 1권은 그것을 쓰게 된 동기를 밝히면서 시작한다. 그 동기는 나우크라테스라는 기하학자의 부탁으로 쓴 것이다. 4권~7권은 페르가뭄 왕 아탈루스에게 감사하는 말로 시작하고, 첫 네 권은 초보적 입문 편이라고 하는 것을 보아 그 내용의 많은 부분은 이미 그 이상의 원뿔곡선에 관한 논문에 실렸던 것으로 보인다.
아폴로니우스가 원뿔곡선의 본질을 넘어선다고 하는 뒤쪽 네 권은 원뿔곡선을 더욱 전문화한 것으로 보인다. 아폴로니우스 이전에는 타원, 포물선, 쌍곡선을 꼭지각이 각각 예각, 직각, 둔각인 3개의 다른 직원뿔의 절단면에서 얻었다. 원뿔을 모선에 수직인 평면으로 자르지 않고, 절단면의 기울기를 변화시키는 것만으로도 하나의 원뿔에서 3종류의 원뿔곡선을 모두 얻을 수 있음을 아폴로니우스가 보였다.
이것은 세 종류의 곡선은 서로 연결시킨 중요한 첫 걸음이었다. 덧붙여서 또 하나의 중요한 일반화가 이루어졌는데 원뿔이 반드시 직원뿔일 필요 없아 기울어진 원뿔에서도 원뿔곡선이 만들어짐을 보였다.
마지막으로 아폴로니우스는 똑같은 원뿔 두 개를 꼭짓점을 맞대고 축을 한 직선 위에 놓음으로써 고대의 곡선을 현대의 관점에 좀 더 가깝게 했다. 아폴로니우스는 원본을 다음과 같이 정의했다.
길이가 무한한 직선이 어떤 정점을 지나며 그 점과 같은 평면 위에 있지 않은 원둘레 위의 모든 점을 지나면서 움직일 때, 그 직선의 자취는 이중원뿔이 된다.
이 새로운 정의에 따라 쌍곡선은 오늘날과 같은 두 갈래 곡선이 되었다. 이 곡선을 기하학자들은 한 쌍곡선의 '두 갈래'라 하지 않고 '두 갈래의 쌍곡선'이라고 했다.
6. 원뿔곡선의 이름
아폴로니우스가 원뿔곡선이라고 이름을 바꾼 것은 아주 중요한 의미가 있다. 그 이전에는 예각원뿔(oxytome)의 절단면, 직각원뿔(orthotome)의 절단면, 둔각원뿔(amblytome)의 절단면이라는 용어를 사용했고, 아르키메데스도 사용했다.
타원, 쌍곡선이라는 이름을 만든 사람은 아폴로니우스 였으나 타원, 포물선, 쌍곡선이라는 말은 피타고라스 학파가 넓이를 이용하여 이차방정식을 풀려고 했을 때 사용한 용어를 고쳐 만들었을 것이다. 곧, 타원을 뜻하는 ellipsis(모자람)는 주어진 넓이의 직사각형을 주어진 선분에 적응했을 때 정사각형(또는 조건이 명확한 다른 도형)만큼 모자라는 경우에 쓰였고, 쌍곡선을 뜻하는 hyperbola(남음)는 주어진 넓이가 주어진 선분을 넘는 경우에 쓰였다. 포물선을 뜻하는 parabola(적용, 비교)는 넘지도 모자라지도 않는 것을 뜻한다. 따라서 아폴로니우스는 그 말들을 원뿔곡선의 이름으로 새로운 의미를 붙여 사용한 것이다.
현재 자주 쓰이는 원점을 꼭짓점으로 하는 포물선의 방정식은 \(y^{2}=lx\,(l=2p\,\text{또는}\,l=4p)\)이고 이것은 포물선이 그 위의 어떤 점을 잡아도 세로 좌표 \(y\)로 만드는 정사각형의 넓이는 가로좌표 \(x\)와 매개변수 \(l\)로 만드는 직사각형의 넓이와 같다는 특성이 있다.
마찬가지로 원점을 꼭짓점(타원의 경우는 중심)으로 하는 타원과 쌍곡선의 방정식은 \(\frac{(x\pm a)^{2}}{a^{2}}\pm\frac{y^{2}}{b^{2}}=1\) 또는 \(y^{2}=lx\mp\frac{b^{2}x^{2}}{a^{2}}\,\left(l=\frac{2b^{2}}{a}\right)\)이므로 타원의 경우는 \(y^{2}<lx\), 쌍곡선의 경우는 \(y^{2}>lx\)이다. 그리고 이 부등식이 보여주는 곡선의 특성은 2000년도 넘는 옛날에 아폴로니우스가 이름을 붙인 근거이고 그 이름이 지금까지 여전히 쓰이는 까닭이다.
참고자료:
수학의 역사-상, (칼 B 보이어, 유타 C 메르츠바흐 지음), 양영오, 조윤동 옮김
'수학사 > 수학사(상)' 카테고리의 다른 글
| 수학사 21-페르가의 아폴로니우스(3) (0) | 2022.07.14 |
|---|---|
| 수학사 20-페르가의 아폴로니우스(2) (0) | 2022.07.13 |
| 수학사 18-시라쿠사의 아르키메데스(3) (0) | 2022.07.12 |
| 수학사 17-시라쿠사의 아르키메데스(2) (0) | 2022.07.12 |
| 수학사 16-시라쿠사의 아르키메데스(1) (0) | 2022.07.11 |
