수학사 14-알렉산드리아의 유클리드(2)
5. 제 1권의 내용
유클리드는 처음의 세 명제에서 공준 3의 매우 제한된 해석으로 초등 기하학에서 거리를 떼어낼 때와 같이 컴파스가 자유롭게 쓰이는 것을 보이려고 노력했다(현대의 엄밀한 기준에서 보면 매우 불충분한 가정이다). 그리고 증명할 때 공준을 주로 암암리에 사용했다. 보기를 들어 원론의 명제 1에서는 두 원은 한 점에서 만난다는 것을 증명하지 않고 사용하는데, 이 경우나 비슷한 경우, 공준의 연속성의 원리에 해당하는 것을 더할 필요가 있다.
게다가 유클리드가 보인 공준 1, 2는 서로 다른 두 점을 연결하는 직선의 유일성도 무한성도 보장하지 않는다. 이 두 공준은 다시 그런 직선은 적어도 하나 있고, 이것은 끝점을 갖지 않는다는 사실을 주장할 뿐이다. 그러나 유클리드는 그 유일성과 무한성을 증명 과정에서 마음대로 사용했다.
그 당시 원론은 분명히 초등수학에서 그때까지 집대성된 것 중에서 가장 심사숙고하여 얻은 이론적 성과였다. 그리고 더 정확하게 표현하려는 움직임이 나타나기까지 2000년이 걸렸다.
원론 제 1권의 대부분의 명제는 고등학교에서 기하학을 배운 사람이라면 누구나도 잘 아는 내용이다. 여기에는 삼각형의 합동(그러나 포갬을 정당화하는 공리는 없었다), 자와 컴파스를 이용한 간단한 작도, 삼각형의 각과 변에 대한 부등식, 평행선의 성질(주어진 각을 갖고 주어진 삼각형 또는 직선도형과 넓이가 같은 평행사변형의 작도를 포함한다)에 관한 일련의 정리가 포함되어 있다.
제 1권은 피타고라스 정리와 그 역의 증명으로 끝난다.
유클리드가 피타고라스 정리를 증명한 방식은 오늘날 교과서에 있는 직각삼각형의 빗변에 그은 수선에 의해 생기는 닮은 삼각형의 변의 비를 이용하는 것과 다르다. 약분가능성에 포함된 어려움 때문에 그러한 증명을 피했다(5권에서 단단한 기초 위에서 비례론에 착수했다, 그때까지 비례의 사용은 가능한 피했다). 대신 유클리드는 풍차 또는 공작의 꼬리(또는 새 색시의 의자)라고 불린 도형을 사용해 증명했다.

그 증명은 선분 \(AC\)위의 정사각형이 삼각형 \(FAB\)의 두 배, 곧 삼각형 \(CAD\)의 두 배로 되어 직사각형 \(AL\)과 같고 그리고 \(BC\)위의 정사각형은 삼각형 \(ABK\)의 두 배, 곧 삼각형 \(BCE\)의 두 배로 되어 직사각형 \(BL\)과 같다는 것ㅇ르 보이면 완성된다. 따라서 두 정사각형의 합은 두 직사가곃ㅇ의 합, 곧 \(AB\)위의 정사각형과 같다.
이 증명은 유클리드 자신의 생각으로 보인다. 증명의 초기 형태에 관하서는 여러가지 추측이 있다.
한편 유클리드 시대 이후로는 위의 방법을 대신하는 증명법이 많이 제시되었다.
피타고라스 정리의 역은 '삼각형에서 한 변 위의 정사각형이 삼각형의 나머지 두 변 위의 정사각형의 합과 같다면 나무지 두 변에 끼인 각은 직각이다'는 내용이다.
그런데 현대의 교과서에 실린 피타고라스 정리를 증명하는 연습문제는 정리 자체가 아니라 여전히 증명되지 않는 역을 요구하는 것이다.
원론에는 작은 결함이 많이 보이지만, 논리학상의 주요 성과도 있었다.
6. 기하학적 대수
원론 2권은 얇고 14개의 명제만 있다. 그러나 그 어느것도 지금 교과서에서 사용되지 않고 있으나 유클리드 시대에는 중요한 내용이었다. 오늘날 우리들에게는 그리스의 기하학적 대수 대신 기호대수나 삼각법이 있다.
보기를 들면 2권의 명제 1은 '두 선분이 있고, 이 가운데 선분 하나가 몇 개의 선분으로 나뉜다면, 원래 두 선분으로 둘러싸인 직사각형은 나뉘어지지 않은 선분과 나누어진 선분의 각 부분으로 둘러싸인 직사각형의 합과 같다' 이다. 이 정리는 다음 그림에서

\(AD\cdot(AP+PR+RB)=AD\cdot AP+AD\cdot PR+ AD\cdot RB\)임을 주장한다. 이것은 분배법칙 \(a(b+c+d)=ab+ac+ad\)를 기하학적으로 나타낸 것이다.
또 원론의 뒤쪽 책(5.7권)에는 곱셈의 교환법칙과 결합법칙의 증명도 실려있다.
반면 지금은 양을 문자로 표시하고 이 문자들은 수라고 이해하고 이를 바탕으로 대수적 계산법을 덧붙인다. 유클리드 시대에는 양을 기하학의 공리와 정리를 만족하는 선분으로 보았다.
그리스인은 대수학을 갖지 않았다고 전해지나 우리의 기호대수와 목적이 거의 같은 기하학적 대수로 된 원론 2권이 있었다. 현대대수학 덕분에 양 사이의 관계 조작이 쉬워졌다. 그러나 유클리드식 대수학의 14개 정리에 정동한 그리스 기하학자는 오늘날 기하학자보다 더 쉽게 구적문제에 응용한다.
유클리드의 명제 "만약 선분을 임의로 자르면, 선분 전체 위의 정사각형은 두 부분 위의 정사각형과 두 부분으로 만들어진 직사각형의 두 배의 합과 같다"는 \((a+b)^{2}=a^{2}+2ab+b^{2}\)를 말로 길게 나타낸 것이다. 그러나 알렉산드리아의 학생들에게는 긴 설명이 알기 쉬웠다.
사실 원론에서는 약 한쪽 반이나 할애해서 이것을 증명했다. 다음 설명(2권의 명제 5)은 \(a^{2}-b^{2}=(a+b)(a-b)\)를 돌려서 표현한 것이다.
"어떤 선분을 두 점으로 서로 같은 부분과 같지 않은 두 부분으로 나눌 때, 같지 않은 두 선분으로 둘러싼 직사각형과 두 분할점 사이의 선분을 한 변으로 하는 정사각형의 합은 본래 주어진 선분의 반을 한 변으로 하는 정사각형과 같다"
유크릴드가 이와 관련하여 이용한 그림은 그리스 대수학에서 중요한 역할을 해 왔다.
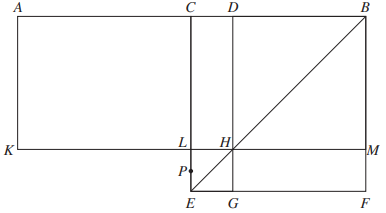
위 그림은 \([AH]+[LG]=[CF]\)를 나타내고, \(AC=CB=a\), \(CD=b\)라 하면 위 그림은 \((a+b)(a-b)+b^{2}=a^{2}\)임을 주장한다. 그러나 위 그림의 중요성은 정리의 증명에 있는 것이 아니라 오히려 이 것과 비슷한 몇 개의 그림을 그리스의 기하학적 대수학자들이 이용했다는 사실이다. 따라서 대수학에서 지금 학생들의 자랑은 (증명가능 여부에 상관없이) 이차방정식을 푸는 것이지만 그리스 학생들은 그것의 기하학 표현이라고 할 수 있는 위 그림과 같은 것을 푸는 것에 자부심을 느꼈다.
그리스 학자가 \(a,\,b\)를 \(a>2b\)인 두 선분으로 \(ax-x^{2}=b^{2}\)를 만족하는 선분 \(x\)를 작도한다면 먼저 선분 \(AB=a\)를 긋고 이것을 점 \(C\)로 이등분했을 것이다. 그리고 점 \(C\)에서 길이가 \(b\)인 수선 \(CP\)를 세우고, \(P\)를 중심으로 하여 반지름이 \(\frac{a}{2}\)인 원을 그려 선분 \(AB\)와 만나는 점을 \(D\)라 했을 것이다.
그 다음으로 \(AB\)위에 \(BM=BD\)인 직사각형 \(ABMK\)를 작도함녀 정사각형 \(BDHM\)이 만들어진다. 이 정사각형의 넓이가 주어진 이차방정식을 만족하는 값 \(x^{2}\)이다.
그런데 여기서 그리스 사람을 따라 선분 \(AB(=a)\)에 주어진 정사각형\((b^{2})\)와 같고 직사각형 \(AM\)보다 정사각형 \(DM\)만큼 작은 직사각형 \(AH(=ax-x^{2})\)를 적용했따.
증명은 앞에서 보인 2권 명제 5를 사용하면 위 그림에서 직사각형 \(ADHK\)는 오목다각형 \(CDFGHL\)과 같다는 것이 확실하다. 즉 다각형 \(CBFGHL\)은 \(\left(\frac{a}{2}\right)^{2}\)보다 정사각형 \(LHGE\)만큼 작고 그 정사각형의 한 변은 원래 그림에서 \(CD=\sqrt{\left(\frac{a}{2}\right)^{2}-b^{2}}\)이다.
이와 마찬가지로 제 2권 명제 6을 사용하여 이차방정식 \(ax+x^{2}=b^{2}\)도 풀고 있다.
"어떤 선분이 이등분되고 임의의 선분이 그 선분과 일직선을 이루게 더해지면(더해진 선분을 포함한) 전체 선분과 더해진 선분을 두 변으로 하는 직사각형과 본래 주어진 선분의 반을 한 변으로 하는 정사각형의 합은 본래의 선분의 반과 더해진 선분을 합친 선분을 한 변으로 하는 정사각형과 같다."
여기서 이제 주어진 직선 \((AB=a)\) 위에 주어진 정사각형\((b^{2})\)과 같고 직사각형 \(AH\)보다 정사각형 1개 만큼 더 큰 직사각형\((AM=ax+x^{2})\)을 적용한다.
이 경우에는 선분 \(CD=\sqrt{\left(\frac{a}{2}\right)^{2}+b^{2}}\)가 되는데 위 명제에서 직사각형 \(AM(=ax+x^{2})\)과 정사각형 \(LG\left(=\left(\frac{a}{2}\right)^{2}\right)\)을 더하면 정사각형 \(CF\left(=\left(\frac{a}{2}\right)^{2}+b^{2}\right)\)와 같다는 것을 알 수 있기 때문이다. 따라서 조건 \(ax+x^{2}=b^{2}\)를 만족한다.
2권 뒤쪽에 정리한 몇 개의 명제는 기하학적 대수의 여러 가지 변형이다. 명제 11은 명제 6의 중요하고 특수한 경우이다. 이때 식 \(ax+x^{2}=a^{2}\)을 풀기 위해 유클리드는 먼저 한 변이 \(a\)인 정사각형 \(ABCD\)를 그리고 변 \(AD\)를 점 \(E\)로 이등분하여 \(E,\,B\)를 잇고 있다. 다음에 변 \(DA\)를 \(EF=EB\)가 되게 \(F\)까지 연장하고 나서 정사각형 \(AFGH\)를 완성한다.

그리고 나서 \(GH\)를 연장하여 선분 \(DC\)와 만나는 점을 \(K\)로 하면, 선분 \(AD\)위에 주어진 정사각형 \(AC(=a^{2})\)와 같고 직사각형 \(AK\)보다도 정사각형 하나((=x^{2}))만큼 큰 직사각형 \(FK(=ax+x^{2})\)를 적용할 것이다(삼각형 \(ABE\)에 피타고라스 정리를 적용하면 \(\left(x+\frac{a}{2}\right)^{2}=\left(\frac{a}{2}\right)^{2}+a^{2}\)).
유클리드는 원론 2권 명제 11에 이용한 그림(위 그림)을 다시 6권 명제 30에서도 이용하는데 이것은 황금분할이 되풀이됨을 보이기 위한 것으로 오늘날 많은 기하학 책에서도 사용한다.
우선 위 그림의 그노몬 \(BCDFGH\)에 점 \(L\)을 더해 큰 직사각형 \(CDFL\)을 완성한다.
(*그노몬: 평행사변형에서 그 한 각을 포함한 닮은 꼴의 작은 평행사변형을 떼어낸 나머지 부분)

이 큰 직사각형 \(LCDF\)와 닮은 직사각형 \(LBHG\)의 변 \(GH\)위에 \(GO=GL\)인 점 \(O\)를 잡아 그노몬 \(BCDFGH\)와 닮은 그노몬 \(LBMNOG\)를 그린다. 다음에 직사각형 \(CDFL\)과 \(LBHG\)와 닮은 더 작은 직사각형 \(BHOP\)안에 그노몬 \(BCDFGH\)와 \(LBMNOG\)와 닮은 그노몬 \(PBHQRN\)을 다시 그린다. 이렇게 계속하면 집적점 \(Z\)에 수렴하는 닮은 직사각형의 축소 무한수열을 얻는다.
여기서 \(Z\)는 선분 \(FB\)와 \(DL\)의 교점임을 쉽게 알 수 있고, 또한 점 \(C,\,A,\,G,\,P,\,M,\,Q,\,...\)에서 직사가곃ㅇ의 변에 접하는 로그나선의 극이기도 하다. 그 밖에도 매력적인 이 그림에서 눈에 띄는 성질 몇 개를 끌어낼 수 있다.
제 12권의 명제 12, 13은 그리스에서 얼마 뒤 싹틀 삼각형에 관한 관심을 암시한다는 점에서 흥미롭다. 이 명제들이 평면삼각형에 대한 코사인 법칙을(둔각->예각) 기하학적으로 공식화했다는 사실을 알게 될 것이다.
명제 12의 둔각삼각형에서 둔각의 대변 위의 정사각형은 둔각을 사이에 끼고 있는 두 변 위의 정사각형의 합 보다 둔각을 끼고 있는 변 하나와 그 변의 연장선에 내린 수선의 연장선과 만나느 점과 둔각의 꼭지점 사이의 선분으로 둘러싸인 직사각형의 두 배 만큼 크다(\(BC^{2}=AB^{2}+AC^{2}+2AB\cdot AD\,(AD=-AC\cos(\angle A))\)).
명제 13. 예각삼각형에서 예각의 대변 위의 정사각형은 예각을 사이에 끼고 있는 두 변 위의 정사각형의 합 보다 예각을 끼고 있는 변의 하나와 그 변에 내린 수선이 이 변을 내분할 때 예각과 가까운 쪽의 선분으로 둘러싸인 직사각형의 두 배 만큼 작다. 즉, 다음과 같다.$$BC^{2}=AB^{2}+AC^{2}-2AB\cdot AD\,(AB=AC\cos(\angle A))$$ 명제 12, 13의 증명에서 피타고라스 정리를 두 번 사용했는데 오늘날의 삼각법에도 자주 보인다.
참고자료:
수학의 역사-상, (칼 B 보이어, 유타 C 메르츠바흐 지음), 양영오, 조윤동 옮김
'수학사 > 수학사(상)' 카테고리의 다른 글
| 수학사 16-시라쿠사의 아르키메데스(1) (0) | 2022.07.11 |
|---|---|
| 수학사 15-알렉산드리아의 유클리드(3) (0) | 2022.07.11 |
| 수학사 13-알렉산드리아의 유클리드(1) (0) | 2022.07.10 |
| 수학사 12-플라톤과 아리스토텔레스(3) (0) | 2022.07.09 |
| 수학사 11-플라톤과 아리스토텔레스(2) (0) | 2022.07.09 |
