수학사 2-이집트
(*분수표기 참고: \(m/n:\frac{m}{n}\))
1. 초기의 기록
금속을 사용한 문명은 이집트, 메소포타미아, 인도, 중국 처럼 하천 유역에서 먼저 발생했다. 나일강 유역과 티그리스와 유프라테스 강의 '기름진 초승달' 지역에 살았던 사람들의 기록은 믿을 수 있다.
기원전 4000년대가 끝나기 앞서 메소포타미아와 나일 강 유역에서 원시적 글자형태가 쓰이기 시작했다. 특히 메소포타미아에서 쐐기문자로 작성된 기록들이 발견되었고, 이 중에서 수학과 관련된 내용은 매우 적다.
2. 신성문자의 기수법
이집트에서는 신성문자로 기록이 작성되었다. 신성문자로 작성된 명수법이 해명되었다. 명수법은 10진법에 기초하고 있다. 10의 1~6제곱까지의 각 거듭제곱을 구별하는 기호와 그것들을 단순히 되풀이하여 나타난 100만을 넘는 수를 돌과 나무 따위에 새겼다.
수직 막대 하나는 1, 거꾸로 된 반원인 쪽문 또는 발뒤꿈치 뼈는 10, 대문자 C와 비슷한 올가미는 100, 연꽃은 1000, 구부러진 손가락은 10000, 올챙이와 비슷한 물고기는 100000, 무릎꿇은 사람은 1000000을 나타낸다.
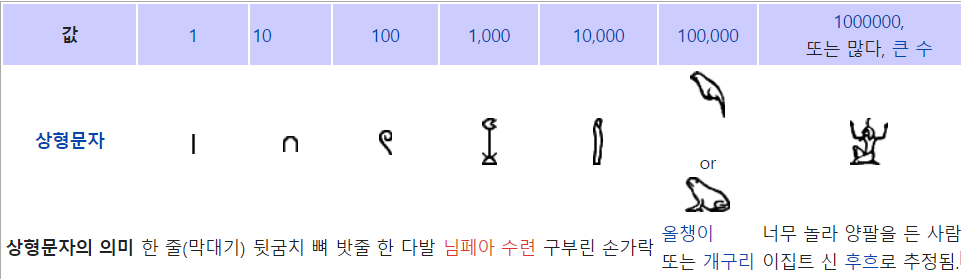
예를들어 12345와 4622는 다음과 같다.

이집트의 비문은 그들이 예로부터 큰 수와 익숙했음을 보여준다. 그 밖의 자료를 보아도 이집트인은 계산과 측정에서 정확함은 분명하다. 때문에 피라미드를 건설하고, 천문학에 흥미를 갖고, 나일강의 홍수가 이리변 시리우스가 태양이 뜨기 전 동쪽 하늘에 나타나면 시작한다는 것을 이미 관측하고, 이 주기가 365일인 것을 알고, 한 달이 30일, 한 해가 12달, 제삿날이 5일인 태양력을 만들었다(실제로 이 역법은 하루의 1/4보다 짧았으므로 네 계절은 4년마다 약 하루 빨라지고, 약 1460년 뒤에 다시 네 계절과 역(曆)이 일치했다).
3. 아메스 파피루스
3500년의 세월을 지나서도 풍화와 파손을 입지 않은 파피루스들이 있다. 파피루스에는 수학에 대한 기록이 있고, 기원전 1650년에 서기 아메스가 쓴 아메스 파피루스와 린드가 구입한 린드 파피루스에도 있다.
린드 파피루스에 기록된 수학과 그 밖의 내용은 신성문자가 아닌 신관문자로 적혀있다. 신관문자에서 1~9까지의 숫자, 10의 거듭제곱은 특별한 기호로 대체되었다.
다음은 4, 7, 28을 이집트 문자로 나타낸 것이다.

4. 단위분수
석기시대 사람들은 분수가 불필요했으나 청동기 시대에는 분수가 필요해졌다. 신성문자는 주로 단위분수(분자가 1인 분수)를 나타내기 위해 분모값을 갖는 정수 위에 달걀 모양을 길게 놓은 기호를 사용했다.

파피루스의 신관문자의 경우, 달걀 모양은 점으로 바뀌고, 대응하는 정수(분모) 위에 놓았다.
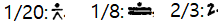
신관문자로 일반분수를 나타내는데는 어려움이 있다. 다만 2/3에는 특별한 신관문자 기호를 부여했고, 때로는 \(1-\frac{1}{n+1}=\frac{n}{n+1}\)형태의 분수도 특수 기호로 나타냈다. 이집트인들은 계산 과정에서 분수 2/3에 특별한 역할을 부여했다.
어떤수의 1/3을 구하기 위해 먼저 그 수의 2/3을 구한 다음 그 반을 취한다. 또한 단위분수 1/p의 2/3는 두 개의 단위분수 1/2p와 1/6p의 합이라는 것과 1/2p를 2배 해서 1/p이 됨을 알고 있었다. 그러나 이집트인들은 m/n꼴의 일반적인 진분수를 기본적인 양으로 생각하지 않고(2/3은 예외) 완성과정에 있는 것으로 보았다.
오늘날 3/5는 기약분수이나 이집트의 서기는 1/3, 1/5, 1/15의 합으로 나뉜다고 생각했다. 그래서 혼합 진분수를 단위 분수의 합으로 린드 파피루스는 5~101 사이의 모든 홀수 \(n\)에 관해 \(\frac{2}{n}\)을 단위분수의 합으로 분해하는 표로 시작하고 있다.
\(\frac{2}{n}\)의 표 가운데 얼마간은 다음의 등식을 이용해서 구했다.$$\frac{2}{n}=\frac{1}{\frac{n+1}{2}}+\frac{1}{\frac{n(n+1)}{2}},\,\frac{2}{pq}=\frac{1}{p\frac{p+q}{2}}+\frac{1}{q\frac{p+q}{2}}$$이집트인들은 자연스런 분수 1/2, 1/3, 1/5를 계속해서 절반으로 나누는 분수를 선호했다고 한다. 또한 \(\frac{2}{3}\cdot\frac{1}{p}=\frac{1}{2p}+\frac{1}{6p}\)을 이용해서 식 \(\frac{2}{15}=\frac{1}{10}+\frac{1}{30}\)을 얻었다.
5. 계산법
아메스 파피루스의 \(\frac{2}{n}\)표 다음에는 1~9의 \(n\)에 대해 \(\frac{n}{10}\)을 나타낸 짧은 표가 있는데 거기에도 단위분수와 \(\frac{2}{3}\)로 표현되어 있다(예: 9/10은 1/30, 1/5, 2/3로 되어있다).
\(\frac{2}{n}\)과 \(\frac{n}{10}\)의 표에 이어지는 파피루스의 주요 부분은 48가지 문제로 되어있고, 그 중 6번 문제는 1, 2, 6, 7, 8, 9개의 빵을 각각 10명에게 나누어 주는 문제인데, 아메스는 \(\frac{n}{10}\)의 표를 이용했다.
한 사람이 한 개의 \(\frac{1}{10}\)을 받으면 두 살마은 \(\frac{2}{10}=\frac{1}{5}\), 네 사람은 \(\frac{2}{5}=\frac{1}{3}+\frac{1}{15}\), 여덟 사람은 \(\frac{2}{3}+\frac{2}{15}=\frac{2}{3}+\frac{1}{10}+\frac{1}{30}\), 여덟사람+두 사람은 \(\frac{2}{3}+\frac{1}{5}+\frac{1}{10}+\frac{1}{30}=1\)이다.
이것으로 보아 아메스는 최소공배수에 버금가는 개념을 알고 있었고, 이에 따라 증명했다. 10명에게 7개의 빵을 나누는 문제에서 1인당 \(\frac{1}{2}+\frac{1}{5}\)개씩 나누어 주어도 되는데 좋아하는 분수 \(\frac{2}{3}\)를 써서 한 개의 \(\frac{2}{3}+\frac{1}{30}\)로 하고 있다.
이집트의 기본 계산법은 덧셈이고, 우리의 곱셈, 나눗셈은 아메스 시대에는 연속해서 2배 하는 것을 되풀이 함으로써 설명했다.$$\begin{align*}69\times19&=69\times(16+2+1)\\&=1104+138+69\\&=1311\\ \left(\frac{1}{16}+\frac{1}{112}\right)&\left(1+\frac{1}{2}+\frac{1}{4}\right)=\frac{1}{8}\end{align*}$$나눗셈의 경우, 2배의 되풀이가 역으로 이루어져 곱하는 수 대신 나누는 수가 연속으로 2배가 되고 있다.
100을 \(7+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\)로 나눈 몫 \(12+\frac{2}{3}+\frac{1}{42}+\frac{1}{126}\)을 다음과 같이 얻었다.
나누는 수를 연속으로 2배 하면 차례로 \(15+\frac{1}{2}+\frac{1}{4},\,13+\frac{1}{2},\,63\)을 얻는다. 마지막 것은 나누는 수의 8배이다. 나누는 수의 \(\frac{2}{3}\)은 \(5+\frac{1}{4}\)이다. 그러므로 나누는 수의 \(8+4+\frac{2}{3}\)를 곱하면 \(99\frac{3}{4}\left(=63+31+\frac{1}{2}+5+\frac{1}{4}\right)\)을 얻는데 이것은 구하는 100에서 \(\frac{1}{4}\)가 모자라다.
여기서 교묘한 조정이 이루어지는데 나누는 수의 8배가 63이므로 나누는 수에 \(\frac{2}{63}\)을 곱하면 \(\frac{1}{4}\)이 생긴다.
\(\frac{2}{n}\)표에서 \(\frac{2}{63}=\frac{1}{42}+\frac{1}{126}\)이므로 구하는 몫은 \(12+\frac{2}{3}+\frac{1}{42}+\frac{1}{126}\)이다.
6. 대수학 문제
이집트에서 \(a,\,b,\,c\)는 알고있는 수, \(x\)는 미지수일 때 \(x+ax=b\) 또는 \(x+ax+bx=c\)와 같은 1차방정식의 해를 구하고 있다. 이때 미지수를 아하(쌓아놓은 더미, aha)라고 한다.
24번 문제는 \(aha+\frac{1}{7}aha=19\)에서 \(aha\)가 얼마인지 구하는 문제이다.
위 문제에 대한 아메스의 풀이법은 현대 교과서와 달리 '가정법'으로 알려진 방법 특유의 순서를 밟고 있다. 정확한 값이 아닌 특정 값을 아하로 가정하고, 좌변에 보이는 연산의 결과를 가정한 수에 실행한다. 그리고 연산의 결과를 바라는 결과와 견주고, 비례법을 사용하여 맞는 답을 찾는다.
위 문제의 경우 원하는 답 19 대신 \(x+\frac{1}{7}x=8\)이 되도록 미지수 가정값을 7로 한다. 그런데 \(8\left(2+\frac{1}{4}+\frac{1}{8}\right)=19\)이므로 바른 답은 7에 \(2+\frac{1}{4}+\frac{1}{8}\)을 곱해야 한다.
아메스는 이 답을 \(16+\frac{1}{2}+\frac{1}{8}\)로 했고, 검산을 통해 \(16+\frac{1}{2}+\frac{1}{8}\)에 그것의 \(\frac{1}{7}\left(=2+\frac{1}{4}+\frac{1}{8}\right)\)을 더하면 19가 되는 것을 확인했다.
검산은 수학에서 하나의 중요한 한 걸음으로 간단한 증명의 한 예이다.
37번 문제 \(x+\frac{2}{3}x+\frac{1}{2}x+\frac{1}{7}x=37\)을 가정법을 사용하지 않고 37을 \(1+\frac{2}{3}+\frac{1}{2}+\frac{1}{7}\)로 나누어 \(16+\frac{1}{56}+\frac{1}{679}+\frac{1}{776}\)이라는 결과를 얻었다.
7. 기하학 문제
그리스 역사가 헤로도투스에 따르면 나일강의 홍수로 인한 경계의 유실이 측량의 필요성을 촉발시켰다고 기록했다. 그러나 이 기록은 과대평가라고 봐야 한다.
고대 이집트 파피루스(아메스 파피루스)에는 기하학 문제가 많다. 그러나 현대의 넓이 구하기와 비교했을 때 부정확하게 구하는 기하학 공식들이 다수였다.
8. 결론
아리스토텔레스는 기하학은 나일강 유역에서 일어났다고 주장했다. 그리스인들이 이집트로부터 초등 수학의 일부를 빌렸다고 할 수 있으나 이집트인들은 기하학을 제대로 활용하지 못했다.
참고자료:
수학의 역사-상, (칼 B 보이어, 유타 C 메르츠바흐 지음), 양영오, 조윤동 옮김
'수학사 > 수학사(상)' 카테고리의 다른 글
| 수학사 6-이오니아와 피타고라스 학파(2) (0) | 2022.07.06 |
|---|---|
| 수학사 5-이오니아와 피타고라스 학파(1) (0) | 2022.07.06 |
| 수학사 4-메소포타미아(2) (0) | 2022.07.05 |
| 수학사 3-메소포타미아(1) (0) | 2022.07.05 |
| 수학사 1-기원 (0) | 2022.07.03 |
