반응형
복소해석학을 이용한 이상적분의 계산(2)
여기서 다루고자 하는 이상적분$$\int_{-\infty}^{\infty}{e^{-zx^{2}-ibx}dx}=\left(\frac{\pi}{z}\right)^{\frac{1}{2}}e^{-\frac{b^{2}}{4z}}\,(z\in\mathbb{C},\,\text{Re}z>0,\,b\in\mathbb{R})$$은 양자역학, 확률론, 파인만적분에 이용되는 공식인데 그 유도는 복소해석학을 이용하지만 과정은 길고 복잡하다. 때문에 앞에서 같이 다루지 않고 여기서 따로 다루도록 하겠다.
다음은 이 적분공식을 유도하는데 필요한 정의와 정리들이다.
1. \(\displaystyle\int_{-\infty}^{\infty}{e^{-ax^{2}}dx}=\sqrt{\frac{\pi}{a}}\,(a>0)\)
2. 지배수렴정리
\(\{f_{n}\}\)을 실수(\(\mathbb{R}\)) 위에서의 연속함수열로 다음이 성립한다고 하자.$$\lim_{n\,\rightarrow\,\infty}{f_{n}(x)}=f(x)$$여기서 \(f\)는 실수 전체에서 연속인 함수이다. 실수 전체에서 적분가능한 함수 \(g\)가 존재해서 다음이 성립하면$$|f_{n}(x)|\leq g(x)\,(x\in\mathbb{R},\,n\in\mathbb{N})$$\(f\)는 실수 전체에서 적분가능하고 다음의 등식이 성립한다$$\lim_{n\,\rightarrow\,\infty}{\int_{-\infty}^{\infty}{f_{n}(x)dx}}=\int_{-\infty}^{\infty}{f(x)dx}$$3. 푸비니 정리
함수 \(f:\mathbb{R}^{2}\,\rightarrow\,\mathbb{R}\)를 영역 \(R\subset\mathbb{R}^{2}\)위에서의 연속함수라 하자.
(i) \(R=\{(x,\,y)\,|\,a\leq x\leq b,\,g_{1}(x)\leq y\leq g_{2}(x)\}\)(\(g_{1},\,g_{2}\)는 \([a,\,b]\)에서 연속)이면 다음이 성립한다.$$\iint_{R}{f(x,\,y)dA}=\int_{a}^{b}{\int_{g_{1}(x)}^{g_{2}(x)}{f(x,\,y)dy}dx}$$(ii) \(R=\{(x,\,y)\,|\,c\leq y\leq d,\,h_{1}(y)\leq x\leq h_{2}(y)\}\)(\(h_{1},\,h_{2}\)는 \([c,\,d]\)에서 연속)이면 다음이 성립한다.$$\iint_{R}{f(x,\,y)dA}=\int_{c}^{d}{\int_{h_{1}(y)}^{h_{2}(y)}{f(x,\,y)dx}dy}$$4. 복소함수 \(f\)가 한 점 \(z_{0}\)에서 연속일 필요충분조건은 \(z_{0}\)로 수렴하는 임의의 수열 \(\{z_{n}\}\)에 대해 \(\displaystyle\lim_{n\,\rightarrow,\,\infty}{f(z_{n})}=f(z_{0})\)가 성립하는 것이다.
5. 복소함수 \(f\)가 \(z_{0}\)에서 해석적이라는 것은 \(z_{0}\)의 한 근방 위의 모든 점에서 미분가능하다는 것이다. \(f\)가 복소평면 \(\mathbb{C}\) 전체에서 해석적이면, 정함수라고 한다.
6. 복소함수 \(f\)가 영역 \(D\) 전체에서 해석적이고 \(D\) 내부에 포함되는 어떤 영역 또는 선분 위에서 \(f(z)=0\)이라 하자. 그러면 \(D\) 전체에서 \(f(z)=0\)이다.
7. 곡선 \(C:z=z(t)\,(a\leq t\leq b)\)위에서 복소함수 \(f\)의 선적분은 다음과 같이 정의된다.$$\int_{C}{f(z)dz}=\int_{a}^{b}{f(z(t))z'(t)dt}$$8. ML-부등식
복소함수 \(f\)가 곡선 \(C\)위의 임의의 점 \(z\)에 대해 \(M>0\)이 존재해서 \(|f(z)|\leq M\), \(C\)의 길이를 \(L\)이라 하자. 그러면 다음의 부등식이 성립한다.$$\left|\int_{C}{f(z)dz}\right|\leq ML$$8. 코시-구르사 정리
\(f\)를 닫힌 곡선 \(C\)와 그 내부에서 해석적이라고 하자. 그러면 다음이 성립한다.$$\int_{C}{f(z)dz}=0$$9. 모레라 정리
복소함수 \(f\)가 \(D\) 전체에서 연속이라 하고, \(D\) 내부의 모든 닫힌곡선 \(C\)에 대해 다음이 성립한다고 하자.$$\int_{C}{f(z)dz}=0$$그러면 \(f\)는 \(D\)전체에서 해석적이다.
다음은 여기서 유도하고자 하는 적분공식이다.
\(\mathbb{C}_{+}=\{z\in\mathbb{C}\,|\,\text{Re}z>0\}\)일 때 \(z\in\mathbb{C}_{+}\)와 \(b\in\mathbb{R}\)에 대하여$$\int_{-\infty}^{\infty}{e^{-zx^{2}-ibx}dx}=\left(\frac{\pi}{z}\right)^{\frac{1}{2}}e^{-\frac{b^{2}}{4z}}$$그 전에 앞서 \(a>0,\,b\in\mathbb{R}\)일 때 다음의 적분공식이 성립함을 보여야 한다.$$\int_{-\infty}^{\infty}{e^{-ax^{2}-ibx}dx}=\sqrt{\frac{\pi}{a}}e^{-\frac{b^{2}}{4a}}$$\(b=0\)이면 1에 의해$$\int_{-\infty}^{\infty}{e^{-ax^{2}}dx}=\sqrt{\frac{\pi}{a}}$$이므로 \(b\neq0\)이라 하자.
(i) \(b>0\)일 때 \(\displaystyle b_{1}=\frac{b}{2a},\,R>0\)이라 하고 다음의 그림을 고려하자.
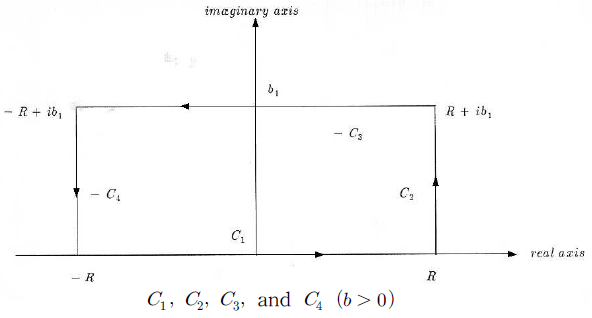
위 그림의 \(C_{1},\,C_{2},\,C_{3},\,C_{4}\)는 다음과 같이 나타낼 수 있고$$C_{1}:z=t\,(-R\leq t\leq R),\,C_{2}:z=R+ti\,(0\leq t\leq b_{1}),\,C_{3}:z=t+b_{1}i\,(-R\leq t\leq R),\,C_{4}:z=-R-ti\,(-b_{1}\leq t\leq0)$$\(C=C_{1}\cup C_{2}\cup-C_{3}\cup C_{4}\)라 하면 \(e^{-az^{2}}\)는 정함수이므로 코시-구르사 정리에 의해 다음이 성립한다.$$0=\int_{C}{e^{-az^{2}}dz}=\int_{C_{1}}{e^{-az^{2}}dz}+\int_{C_{2}}{e^{-az^{2}dz}}-\int_{C_{3}}{e^{-az^{2}}dz}+\int_{C_{4}}{e^{-az^{2}}dz}$$이때$$\begin{align*}\int_{C_{3}}{e^{-az^{2}}dz}&=\int_{-R}^{R}{e^{-a(t+b_{1}i)^{2}}dt}=\int_{-R}^{R}{e^{-a(t^{2}+2b_{1}ti-b_{1}^{2})}dt}\\ \int_{C_{1}}{e^{-az^{2}}dz}&=\int_{-R}^{R}{e^{-at^{2}}dt}\end{align*}$$이고$$\begin{align*}\int_{C_{2}}{e^{-az^{2}}dz}&=i\int_{0}^{b_{1}}{e^{-a(R+ti)^{2}}dt}=i\int_{0}^{b_{1}}{e^{-a(R^{2}+2Rti-t^{2})}dt}\\&=ie^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}e^{-2aRti}dt}\\ \int_{C_{4}}{e^{-az^{2}}dz}&=-i\int_{-b_{1}}^{0}{e^{-a(R+ti)^{2}}dt}=-i\int_{-b_{1}}^{0}{e^{-a(R^{2}+2Rti-t^{2})}dt}=-ie^{-aR^{2}}\int_{-b_{1}}^{0}{e^{-2aRt}e^{at^{2}}dt}\\&=-ie^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}e^{2aRti}dt}\end{align*}$$이므로 다음이 성립한다.$$\begin{align*}0&=\int_{-R}^{R}{e^{-at^{2}}dt}-\int_{-R}^{R}{e^{-a(t^{2}+2b_{1}ti-b_{1}^{2})}dt}+ie^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}e^{-2aRti}dt}-ie^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}e^{2aRti}dt}\\&=\int_{-R}^{R}{e^{-at^{2}}dt}-\int_{-R}^{R}{e^{-a(t^{2}+2b_{1}ti-b_{1}^{2})}dt}+2e^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}\sin2aRt dt}\end{align*}$$이때$$\left|2e^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}\sin2aRt dt}\right|\leq2e^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}dt},\,\lim_{R\,\rightarrow\,\infty}{2e^{-aR^{2}}\int_{0}^{b_{1}}{e^{at^{2}}dt}}=0$$이므로 다음의 등식이 성립한다.$$\int_{-\infty}^{\infty}{e^{-at^{2}-2b_{1}ati+ab_{1}^{2}}dt}=\int_{-\infty}^{\infty}{e^{-at^{2}}dt}=\sqrt{\frac{\pi}{a}}$$\(\displaystyle b_{1}=\frac{b}{2a}\)이므로 \(\displaystyle ab_{1}^{2}=\frac{b^{2}}{4a}\)이고 따라서 \(b>0\)일 때 다음의 결과를 얻는다.$$\int_{-\infty}^{\infty}{e^{-ax^{2}-ibx}dx}=\sqrt{\frac{\pi}{a}}e^{-\frac{b^{2}}{4a}}$$(ii) \(b<0\)일 때 \(\displaystyle b_{1}=\frac{b}{2a}\)라 하고 다음의 그림을 고려하자.

위 그림의 \(C_{1},\,C_{2},\,C_{3},\,C_{4}\)는 다음과 같이 나타낼 수 있고$$C_{1}:z=t+b_{1}i\,(-R\leq t\leq R),\,C_{2}:z=R+ti\,(b_{1}\leq t\leq0),\,C_{3}:z=-t\,(-R\leq t\leq R),\,C_{4}:z=-R-ti\,(0\leq t\leq-b_{1})$$\(C=C_{1}\cup C_{2}\cup C_{3}\cup C_{4}\)라 하면 \(e^{-az^{2}}\)는 정함수이므로 코시-구르사 정리에 의해 다음이 성립한다.$$0=\int_{C}{e^{-az^{2}}dz}=\int_{C_{1}}{e^{-az^{2}}dz}+\int_{C_{2}}{e^{-az^{2}}dz}+\int_{C_{3}}{e^{-az^{2}}dz}+\int_{C_{4}}{e^{-az^{2}}dz}$$이때$$\begin{align*}\int_{C_{1}}{e^{-az^{2}}dz}&=\int_{-R}^{R}{e^{-a(t+b_{1}i)^{2}}dt}=\int_{-R}^{R}{e^{-a(t^{2}+2b_{1}ti-b_{1}^{2})}dt}\\ \int_{C_{3}}{e^{-az^{2}}dz}&=-\int_{-R}^{R}{e^{-at^{2}}dt}\end{align*}$$이고$$\begin{align*}\int_{C_{2}}{e^{-az^{2}}dz}&=i\int_{b_{1}}^{0}{e^{-a(R+ti)^{2}}}=i\int_{b_{1}}^{0}{e^{-a(R^{2}+2Rti-t^{2})}dt}\\&=ie^{-aR^{2}}\int_{b_{1}}^{0}{e^{at^{2}}e^{-2aRti}dt}\\ \int_{C_{4}}{e^{-az^{2}}dz}&=-i\int_{0}^{-b_{1}}{e^{-a(R+ti)^{2}}dt}=-i\int_{0}^{-b_{1}}{e^{-a(R^{2}+2Rti-t^{2})}dt}=-ie^{-aR^{2}}\int_{0}^{-b_{1}}{e^{at^{2}}e^{-2aRti}dt}\\&=-ie^{-aR^{2}}\int_{b_{1}}^{0}{e^{at^{2}}e^{2aRti}dt}\end{align*}$$이므로 다음이 성립한다.$$\begin{align*}0&=-\int_{-R}^{R}{e^{-at^{2}}dt}+\int_{-R}^{R}{e^{-a(t^{2}+2b_{1}ti-b_{1}^{2})}dt}+ie^{-aR^{2}}\int_{b_{1}}{0}{e^{at^{2}}e^{-2aRti}dt}-ie^{-aR^{2}}\int_{b_{1}}^{0}{e^{at^{2}}e^{2aRti}dt}\\&=-\int_{-R}^{R}{e^{-at^{2}}dt}+\int_{-R}^{R}{e^{-a(t^{2}+2b_{1}ti-b_{1}^{2})}dt}+2e^{-aR^{2}}\int_{b_{1}}^{0}{e^{at^{2}}\sin2aRt dt}\end{align*}$$이때$$\left|2e^{-aR^{2}}\int_{b_{1}}^{0}{e^{at^{2}}\sin2aRtdt}\right|\leq2e^{-aR^{2}}\int_{b_{1}}^{0}{e^{at^{2}}dt},\,\lim_{R\,\rightarrow\,\infty}{2e^{-aR^{2}}\int_{b_{1}}^{0}{e^{at^{2}}dt}}=0$$이므로 다음의 등식이 성립한다.$$\int_{-\infty}^{\infty}{e^{-at^{2}-2ab_{1}ti+ab_{1}^{2}}dt}=\int_{-\infty}^{\infty}{e^{-at^{2}}dt}=\sqrt{\frac{\pi}{a}}$$\(\displaystyle b_{1}=\frac{b}{2a}\)이므로 \(\displaystyle b_{1}^{2}=\frac{b^{2}}{4a}\)이고 따라서 \(b<0\)일 때 다음의 결과를 얻는다.$$\int_{-\infty}^{\infty}{e^{-ax^{2}-ibx}dx}=\sqrt{\frac{\pi}{a}}e^{-\frac{b^{2}}{4a}}$$그러므로 모든 \(a>0,\,b\in\mathbb{R}\)에 대해 다음의 공식이 성립한다.$$\int_{-\infty}^{\infty}{e^{-ax^{2}-ibx}dx}=\sqrt{\frac{\pi}{a}}e^{-\frac{b^{2}}{4a}}$$이제 \(z\in\mathbb{C}_{+},\,b\in\mathbb{R}\)에 대하여 다음의 공식이 성립함을 보이자.$$\int_{-\infty}^{\infty}{e^{-zx^{2}-ibx}dx}=\left(\frac{\pi}{z}\right)^{\frac{1}{2}}e^{-\frac{b^{2}}{4z}}$$\(z\in\mathbb{C}_{+}\)에 대하여 1에 의해$$\int_{-\infty}^{\infty}{|e^{-zx^{2}-ibx}|dx}\leq\int_{-\infty}^{\infty}{e^{-(\text{Re}z)x^{2}}dx}=\sqrt{\frac{\pi}{\text{Re}z}}<\infty$$이므로 적분 \(\displaystyle\int_{-\infty}^{\infty}{e^{-zx^{2}-ibx}dx}\)는 존재한다.$$f(z)=\int_{-\infty}^{\infty}{e^{-zx^{2}-ibx}dx},\,g(z)=\left(\frac{\pi}{z}\right)^{\frac{1}{2}}e^{-\frac{b^{2}}{4z}}\,(z\in\mathbb{C}_{+})$$라 하자. 그러면 \(g(z)\)의 분지 절단을 음의 실수축이라고 하면 \(g(z)\)는 \(\mathbb{C}_{+}\)에서 해석적이다. \(f(z)\)를 \(\mathbb{C}_{+}\)에서 해석적이고 \(z\in\mathbb{C}_{+}\)에 대해 \(h(z)=f(z)-g(z)\)라 하자. 그러면 실수 \(z>0\)에 대하여 \(h(z)=0\)이므로 6에 의해 \(h(z)=0\)이고 따라서 모든 \(z\in\mathbb{C}_{+}\)에 대하여 \(f(z)=g(z)\)가 성립한다.
그러므로 \(f(z)\)가 \(\mathbb{C}_{+}\)위에서 해석적임을 보이면 된다.
\(C:z(t)=x_{1}(t)+iy(t)\,(a\leq t\leq b)\)를 \(\mathbb{C}_{+}\)위의 닫힌곡선, \(\displaystyle M=\inf_{a\leq t\leq b}{x_{1}(t)}\)라 하자. 그러면 \(C\)는 \(\mathbb{C}_{+}\)위에서 닫힌 곡선이므로 \(M>0\)이다.$$\int_{C}{f(z)dz}=\int_{a}^{b}{\left(\int_{-\infty}^{\infty}{e^{-\{x_{1}(t)+iy(t)\}x^{2}-ibx}dx}\right)z'(t)dt}$$이고$$\begin{align*}&\int_{a}^{b}{\int_{-\infty}^{\infty}{|e^{-\{x_{1}(t)+iy(t)\}x^{2}-ibx}|\left|z'(t)\right|dx}dt}\\&\leq\int_{a}^{b}{\int_{-\infty}^{\infty}{e^{-x_{1}(t)x^{2}}\left|z'(t)\right|dx}dt}\\&\leq\int_{a}^{b}{\int_{-\infty}^{\infty}{e^{-Mx^{2}}}\left|z'(t)\right|dxdt}\\&=\sqrt{\frac{\pi}{M}}\int_{a}^{b}{\left|z'(t)\right|dt}\\&=L\sqrt{\frac{\pi}{M}}<\infty\,\left(L=\int_{a}^{b}{|z'(t)|dt}\right)\end{align*}$$이며, \(e^{-zx^{2}}\)는 정함수 이므로 푸비니 정리(3)와 코시-구르사 정리(8)에 의해$$\begin{align*}\int_{C}{f(z)dz}&=\int_{a}^{b}{\left(\int_{-\infty}^{\infty}{e^{-\{x_{1}(t)+iy(t)\}x^{2}-ibx}dx}\right)z'(t)dt}\\&=\int_{-\infty}^{\infty}{e^{-ibx}\left(\int_{C}{e^{-zx^{2}}dz}\right)dx}\\&=0\end{align*}$$이다.
\(f(z)\)가 \(\mathbb{C}_{+}\)에서 연속임을 보이자.
\(z_{0}\in\mathbb{C}_{+}\), \(\{z_{n}\}\)을 \(z_{0}\)로 수렴하는 임의의 \(\mathbb{C}_{+}\)위에서의 수열이라고 하자. 즉, \(\displaystyle\lim_{n\,\rightarrow\,\infty}{z_{n}}=z_{0}\)
\(N\in\mathbb{N}\)을 선택해서 모든 \(n>N\)에 대해 \(\displaystyle|z_{n}-z_{0}|<\frac{\text{Re}z_{0}}{2}\)이라 하자. 그러면 모든 \(n>N\)에 대해 다음이 성립한다.$$|\text{Re}z_{n}-\text{Re}z_{0}|\leq|z-z_{0}|<\frac{\text{Re}z_{0}}{2},\,\frac{\text{Re}z_{0}}{2}<\text{Re}z_{n}$$\(\displaystyle m=\min\left\{\text{Re}z_{1},\,...,\,\text{Re}z_{N},\,\frac{\text{Re}z_{0}}{2}\right\}\)라 하자. 그러면 모든 \(n\in\mathbb{N}\)에 대하여 \(0<m\leq\text{Re}z_{n}\)이고 따라서 다음이 성립하고$$|e^{-z_{n}x^{2}}|=e^{-(\text{Re}z_{n})x^{2}}\leq e^{-mx^{2}}$$지배수렴정리에 의해$$\begin{align*}\lim_{n\,\rightarrow\,\infty}{f(z_{n})}&=\lim_{n\,\rightarrow\,\infty}{\int_{-\infty}^{\infty}{e^{-z_{n}x^{2}-ibx}dx}}=\int_{-\infty}^{\infty}{\left(\lim_{n\,\rightarrow\,\infty}{e^{-z_{n}x^{2}-ibx}}\right)dx}\\&=\int_{-\infty}^{\infty}{e^{-z_{0}x^{2}-ibx}dx}=f(z_{0})\end{align*}$$이다. 따라서 4에 의해 \(f(z)\)는 \(z_{0}\)에서 연속이고 모레라 정리에 의해 \(f(z)\)는 \(\mathbb{C}_{+}\)에서 해석적이다.
그러므로 모든 \(z\in\mathbb{C}_{+},\,b\in\mathbb{R}\)에 대하여 다음의 공식이 성립한다.$$\int_{-\infty}^{\infty}{e^{-zx^{2}-ibx}dx}=\left(\frac{\pi}{z}\right)^{\frac{1}{2}}e^{-\frac{b^{2}}{4z}}$$참고자료:
Complex Variables and Applications 8th edition, Brown, Churchill, McGraw-Hill
[논문] AN IMPROPER INTEGRAL OF EXPONENTIAL TYPE FUNCTION USING COMPLEX LINE INTEGRALS, 이은선, 경기대학교 교육대학원
반응형
'수학연구소 > 연구소' 카테고리의 다른 글
| 적분으로서의 자연로그 (0) | 2021.01.28 |
|---|---|
| 복소해석학을 이용한 이상적분의 계산(1) (0) | 2021.01.17 |
| 2차원 벡터장과 복소함수에 대한 고찰 (0) | 2021.01.06 |
| 코시 적분공식과 파생되는 결과들 (0) | 2021.01.02 |
| 르베그-라돈-니코딤 정리의 다양한 증명 (0) | 2021.01.01 |
