4. 논리 게이트
논리 게이트(logic gate)에는 NOT, AND, OR, NAND, NOR, XOR, XNOR게이트가 있다.
NOT 게이트(반전기)
다음은 NOT 게이트의 기호와 진리표이다.
왼쪽의 삼각형 모양의 기호가 반전기의 고유기호이고, 가운데의 사각형 모양의 기호도 사용된다. NOT 게이트는 반전기(inverter)로 입력과 반대되는 출력이 나온다. NOT 게이트에 대한 불 식은 \(X=\overline{A}\)(\(A\)는 입력)
위의 그림은 NOT 게이트의 동작을 나타낸 것이고 펄스 입력에 대해 반전된 펄스 출력이 나온다.
아래의 그림은 타이밍 다이어그램(timing diagram)으로 두 개 이상의 파형에 대한 상호 시간관계를 나타낸다.
입, 출력에서의 상승시간, 하강시간은 이상적으로 0이나 실제로는 지연시간에 의해 상승시간, 하강시간은 0보다 크다.
NOT 게이트는 앞에서 다룬 1의 보수 변환에 사용된다.
(8비트 1의 보수회로)
AND 게이트
다음은 AND 게이트의 기호와 진리표이다.
왼쪽의 위의 그림은 AND게이트의 고유 기호이고, 아래쪽 그림은 사각형 모양의 AND게이트 기호이다. AND게이트는 A, B입력이 모두 1인 경우에만 1이 출력되고 나머지의 경우는 전부 0이 출력된다. AND 게이트에 대한 불 식은 \(X=A\cdot B\)(AND)이다.
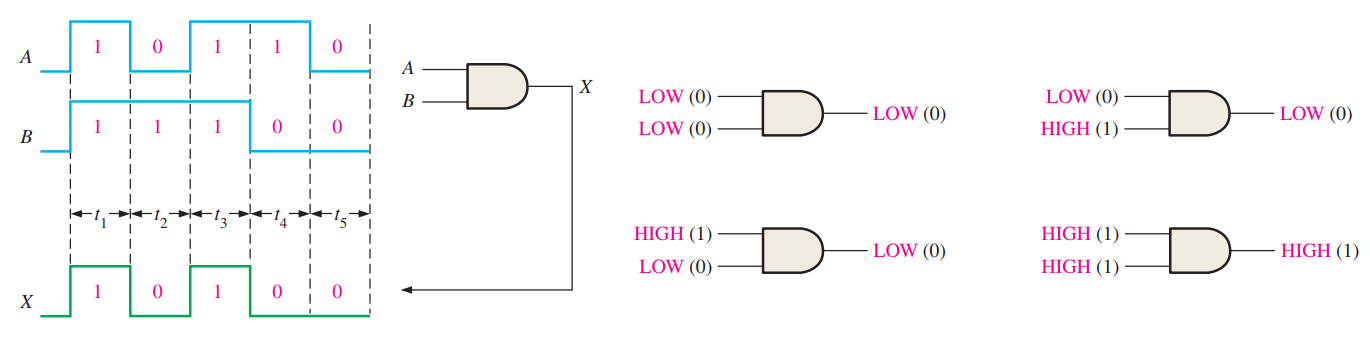
위의 왼쪽 그림은 펄스 입력에 따른 AND 게이트의 출력을 나타낸 것이고, 오른쪽은 각 입력의 경우에 대한 출력을 나타낸 것이다.
OR게이트
다음은 OR 게이트의 기호와 진리표이다.
왼쪽의 위의 그림은 OR게이트의 고유 기호이고, 아래쪽 그림은 사각형 모양의 OR게이트 기호이다. OR게이트는 A, B입력이 모두 0인 경우에만 0이 출력되고 나머지의 경우는 전부 1이 출력된다. OR 게이트에 대한 불 식은 \(X=A+B\)(OR)이다.
위의 왼쪽 그림은 펄스 입력에 따른 OR 게이트의 출력을 나타낸 것이고, 오른쪽은 각 입력의 경우에 대한 출력을 나타낸 것이다.
NAND 게이트
다음은 NAND 게이트의 기호와 진리표이다.
왼쪽 위의 그림은 NAND게이트의 고유 기호이고, 가운데의 NOT/AND 게이트와 등가(물리적으로 같은 게이트)이다. 왼쪽 아래의 그림은 사각형 모양의 NAND 게이트 기호이다. NAND 게이트는 A, B입력이 모두 1인 경우에만 0이 출력되고 나머지의 경우는 전부 1이 출력된다. NAND 게이트에 대한 불 식은 \(X=A\uparrow B=\overline{A\cdot B}(=\overline{A}+\overline{B})\)이다.
위의 왼쪽 그림은 펄스 입력에 따른 NAND 게이트의 출력을 나타낸 것이고, 오른쪽은 각 입력의 경우에 대한 출력을 나타낸 것이다.
위의 그림은 NAND 게이트가 NOT-OR 게이트와 등가임을 나타낸 것이다. 그 이유는 NAND 게이트의 불 식은 \(X=\overline{A\cdot B}=\overline{A}+\overline{B}\)이고, NOT-OR 게이트의 불 식은 \(X=\overline{A}+\overline{B}\)이기 때문이다.
NOR 게이트
다음은 NOR 게이트의 기호와 진리표이다.
왼쪽 위의 그림은 NOR게이트의 고유 기호이고, 가운데의 NOT/OR 게이트와 등가(물리적으로 같은 게이트)이다. 왼쪽 아래의 그림은 사각형 모양의 NOR 게이트 기호이다. NOR 게이트는 A, B입력이 모두 0인 경우에만 1이 출력되고 나머지의 경우는 전부 0이 출력된다. NOR 게이트에 대한 불 식은 \(X=A\downarrow B=\overline{A+B}(=\overline{A}\cdot\overline{B})\)이다.
위의 왼쪽 그림은 펄스 입력에 따른 NOR 게이트의 출력을 나타낸 것이고, 오른쪽은 각 입력의 경우에 대한 출력을 나타낸 것이다.
위의 그림은 NOR 게이트가 NOT-AND 게이트와 등가임을 나타낸 것이다. 그 이유는 NOR 게이트의 불 식이 \(X=\overline{A+B}=\overline{A}\cdot\overline{B}\)이고 NOT-AND 게이트의 불 식이 \(X=\overline{A}\cdot\overline{B}\)이기 때문이다.
XOR 게이트
다음은 XOR(exclusive-OR) 게이트의 기호와 진리표를 나타낸 것이다.
왼쪽 위의 그림은 XOR게이트의 고유 기호이고, 왼쪽 아래의 그림은 사각형 모양의 XOR 게이트 기호이다. XOR 게이트는 A, B입력이 모두 0, 1인 경우에만 0이 출력되고 나머지의 경우는 전부 1이 출력된다. XOR 게이트에 대한 불 식은 \(X=A\oplus B\)이다.
위의 왼쪽 그림은 펄스 입력에 따른 XOR 게이트의 출력을 나타낸 것이고, 오른쪽은 각 입력의 경우에 대한 출력을 나타낸 것이다.
XNOR 게이트
다음은 XNOR(exclusive-NOR) 게이트의 기호와 진리표를 나타낸 것이다.
왼쪽 위의 그림은 XNOR게이트의 고유 기호이고, 왼쪽 아래의 그림은 사각형 모양의 XNOR 게이트 기호이다. XNOR 게이트는 A, B입력이 모두 0, 1인 경우에만 1이 출력되고 나머지의 경우는 전부 0이 출력된다. XNOR 게이트에 대한 불 식은 \(X=A\odot B\)이다.
위의 그림은 XNOR 게이트의 각 입력의 경우에 대한 출력을 나타낸 것이다.
XOR 게이트는 다음과 같이 2비트 가산기로 사용할 수 있다.
다입력 논리게이트
AND, OR 게이트의 경우
(다입력 AND, OR 게이트)
교환법칙: \(x\cdot y=y\cdot x,\,x+y=y+x\)
결합법칙: \((x\cdot y)\cdot z=x\cdot(y\cdot z),\,(x+y)+z=x+(y+z)\)
이므로 AND, OR 게이트에 대해서 교환법칙과 결합법칙이 성립하고 따라서 다입력으로 확장이 가능하다.
반면 NAND, NOR 게이트의 경우$$(x\uparrow y)\uparrow z=\overline{(\overline{(x\cdot y)}\cdot z)}=x\cdot y+\overline{z},\,x\uparrow(y\uparrow z)=\overline{(x\cdot\overline{(y\cdot z)})}=\overline{x}+y\cdot z$$이고$$\begin{align*}(x\downarrow y)\downarrow z&=\overline{(\overline{(x+y)}+z)}=(x+y)\cdot\overline{z}=x\cdot\overline{z}+y\cdot\overline{z}\\x\downarrow(y\downarrow z)&=\overline{(x+\overline{(y+z)})}=\overline{x}\cdot(y+z)=\overline{x}\cdot y+\overline{x}\cdot z\end{align*}$$이므로 NAND, NOR 게이트에 대해서 교환법칙과 결합법칙이 성립하지 않고 반드시 다입력 NAND, NOR 게이트를 사용해야 한다.
다입력 NAND, NOR 게이트:$$x\uparrow y\uparrow z=\overline{x\cdot y\cdot z},\,x\downarrow y\downarrow z=\overline{x+y+z}$$
XOR, XNOR 게이트의 경우
교환법칙: \(x\oplus y=y\oplus x,\,x\odot y=y\odot x\)
결합법칙: \(x\oplus(y\oplus z)=(x\oplus y)\oplus z,\,x\odot(y\odot z)=(x\odot y)\odot z\)
이므로 XOR, XNOR 게이트에 대해서 교환법칙과 결합법칙이 성립한다. 그러나 다입력 XOR, XNOR 게이트는 하드웨어적인 측면에서 일반적이지 못하다.
다음의 그림은 DIP와 SOIC의 패키지이다.
IC의 동작특성
전달지연에 의해 스위칭 속도가 결정되고 전달지연은 스위칭 속도의 역수이다.
전달지연시간(propagation delay time)은 입력 펄스의 변화에 따른 출력 펄스의 변화가 일어나기 까지 시간차이고 다음의 두 가지 시간이 있다.
\(t_{PHL}\)은 출력이 HIGH에서 LOW로 변할 때 입력펄스의 기준점으로부터 출력펄스의 기준점까지의 시간간격이고, \(t_{PLH}\)는 출력이 LOW에서 HIGH로 변할 때 입력펄스의 기준점으로부터 출력펄스의 기준점까지의 시간간격이다.
다음은 NOT 게이트의 지연시간을 나타낸 것이다.
전력소모는 직류 공급전원의 전압 \(V_{CC}\)와 평균 공급전류 \(I_{CC}\)의 곱으로 정의되고, \(I_{CCL}\)을 출력이 LOW일 때의 \(I_{CC}\)의 값, \(I_{CCH}\)를 출력이 HIGH일 때의 \(I_{CC}\)의 값이라고 하면 \(I_{CCL}>I_{CCH}\)이고 \(I_{CC}\)의 평균값은 \(\displaystyle\frac{1}{2}I_{CCL},\,\frac{1}{2}I_{CCH}\)이다.
출력 레벨을 적정수준으로 유지하면서 구동할 수 있는 IC의 논리 입력의 개수를 팬-아웃(fan-out)이라고 한다. 팬-아웃을 초과하면 정상적인 동작을 보장할 수 없다(구동전류가 나누어서 흐르기 때문에 논리 게이트를 구동할 수 없다).
속도-전력 곱(speed-power product, SPP)을 전달지연시간과 전력소모의 곱으로 정의하고, 논리게이트의 성능을 평가하는 척도로 사용된다. 곱의 값이 작을수록 성능이 좋음을 뜻한다.
논리 게이트의 규격서
논리 게이트의 규격서에는 권장 동작조건, 전기적 특성, 스위칭 특성이 기록되어 있다. 논리게이트의 규격서에서
\(V_{CC}\): 직류 전원 전압
\(I_{OH}\): 출력이 HIGH일 때 논리 게이트가 부하를 구동하는 출력 전류(source)
\(I_{OL}\): 출력이 LOW일 때 논리 게이트가 부하로부터 받는 출력 전류(sink)
\(V_{IH}\): 게이트의 입력 레벨이 HIGH로 인식되는 전압
\(V_{IL}\): 게이트의 입력 레벨이 LOW로 인식되는 전압
\(V_{OH}\): 게이트의 출력이 HIGH로 출력되는 전압 레벨
\(V_{OL}\): 게이트의 출력이 LOW로 출력되는 전압 레벨
\(I_{IH}\): HIGH 레벨 입력 전압이 인가될 때의 입력 전류
\(I_{IL}\): LOW 레벨 입력 전압이 인가될 때의 입력 전류
\(I_{OS}\): 게이트 출력이 접지와 단락되었을 때의 출력전류(이 때, 입력패턴은 출력이 HIGH가 되도록 인가)
\(I_{CCH}\): 모든 게이트의 출력이 HIGH일 때 \(V_{CC}\)로부터 흐르는 총 전류
\(I_{CCL}\): 모든 게이트의 출력이 LOW일 때 \(V_{CC}\)로부터 흐르는 총 전류
\(t_{PLH}\): 출력이 LOW 에서 HIGH로 변할 때 입력으로부터 출력까지의 지연시간
\(t_{PHL}\): 출력이 HIGH 에서 LOW로 변할 때 입력으로부터 출력까지의 지연시간
이다. 다음은 논리회로의 규격서이다.
54/74HC00A NAND quad 2-input 게이트에 대한 규격서
54/74LS00 quad 2-input NAND 게이트의 규격서
참고자료:
Digital Fundamentals 11th edition, Floyd, Pearson
'전자공학 > 디지털논리회로' 카테고리의 다른 글
| 6. 조합논리 (0) | 2019.04.08 |
|---|---|
| 5. 불 대수, 카르노 맵 (0) | 2019.04.07 |
| 3. BCD, 디지털 코드, 패리티 방법 (0) | 2019.04.05 |
| 2. 2, 8, 16진수 (0) | 2019.04.04 |
| 1. 디지털의 개념, 집적회로(IC)의 종류 (0) | 2019.04.03 |























