[조합론] 4. 점화식(1: 알고리즘, 점화식들의 예)
알고리즘(algorithm)은 주어진 문제를 (컴퓨터를 사용하여) 해결하기 위한 방법을 의미하며 어떤 값 또는 값의 집합을 입력으로 받아 갑 또는 값의 집합을 출력하는 잘 정의도니 절차이다.
다음은 알고리즘의 5가지 특징이다.
(1) 유한성(finiteness): 알고리즘은 유한번 안으로 끝나야 한다.
(2) 명확성(definiteness): 알고리즘의 각 단계는 명확하게 정의되어야 한다.
(3) 입력(input): 알고리즘이 시작되기 위해서는 초기에 어떤 특정한 값을 입력해야 한다.
(4) 출력(output): 알고리즘은 입력과 관계가 있는 몇 개의 출력이 있어야 한다.
(5) 유효성(effectiveness): 알고리즘에서의 모든 작업은 정확해야 하며, 종이와 연필로 유한 시간에 끝낼 수 있어야 한다.
알고리즘에서는 정확성과 효율성 이 두가지를 고려해야 하며, 정확성과 관련해서 고려해야 할 요소는 다음과 같다.
(1) 유한회의 과정을 통해 답을 얻을 수 있어야 한다.
(2) 단계가 분명하게 정의되어 있어야 한다.
(3) 한 단계가 끝나면 다음 단계가 명확해야 한다.
다음은 알고리즘의 예시들이다.
*참고: 다음의 알고리즘은 의사코드(psuedo code)로 작성되었다.
호너의 방법(Horner's method)
호너의 방법은 특정한 \(x\)에 대하여 다항식 \(f(x)=a_{0}x^{n}+a_{1}x^{n-1}+\cdots+a_{n-1}x+a_{n}\)의 값을 구하는 과정이다.
Procedure poly(x) f_{0}=a_{0} for i=0 to n-1 do f_{i+1}=f_{i}×x+a_{i+1} return f_{n} end poly |
여러개의 수 중에서 큰 수를 찾는 알고리즘
algorithm max(a_{1}, a_{2}, ..., a_{n}) begin max=a_{1} i=2 while i<=n { if max<a_{i} then max=a_{i} i=i+1 } print max end |
\(n!\)을 구하는 알고리즘
Procedure factorial(n) if n=0 then return(1) return(n*factorial(n-1)) end factorial |
음이 아닌 두 정수 \(a\)와 \(b\)에 대하여 두 수의 최대공약수를 구하는 알고리즘(유클리드 알고리즘)
Procedure gcd(a, b) if a<b then swap(a, b) #큰 수로 바꾸기# if b=0 then return(a) r=a mod b #r은 a를 b로 나누었을 때의 나머지# return(gcd(b, r)) end gcd |
순서도(flow chart)는 알고리즘을 그림으로 나타낸 것으로, 해결 과정을 단계적으로 쉽게 파악할 수 있게끔 그림(전개도)으로 나타낸 것이다.
다음은 순서도에 사용되는 기호들이다.
|
시작 또는 끝을 나타내는 기호 |
|
처리 기호 |
|
판단기호 |
|
인쇄기호 |
다음은 순서도의 한 예시이다.
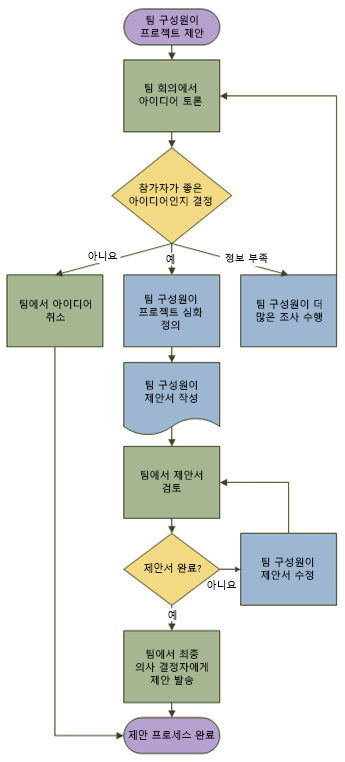
알고리즘의 효율성을 판단하는 기준은 문제를 해결하는데 소요되는 시간이다.
예: 다음은 \(n\)개의 수 \(x_{1},\,x_{2},\,\cdots,\,x_{n}\)을 크기순으로 배열하는 두가지 방법이다.
방법 1
1. 다음 알고리즘에 의해 \(x_{1},\,x_{2},\,\cdots,\,x_{n}\)의 최댓값 \(\max\{x_{1},\,x_{2},\,\cdots,\,x_{n}\}\)을 찾는다.
(1) \(x_{1}\)과 \(x_{2}\)를 비교하여 \(\max\{x_{1},\,x_{2}\}\)를 찾는다.
(2) \(\max\{x_{1},\,x_{2}\}\)와 \(x_{3}\)을 비교하여 \(\max\{x_{1},\,x_{2},\,x_{3}\}\)을 찾는다.
..........................................
(n-1) \(\max\{x_{1},\,x_{2},\,\cdots,\,x_{n-1}\}\)과 \(x_{n}\)을 비교하여 \(\max\{x_{1},\,x_{2},\,\cdots,\,x_{n}\}\)을 찾는다.
2. \(x_{1},\,x_{2},\,\cdots,\,x_{n}\)중 \(\max\{x_{1},\,x_{2},\,\cdots,\,x_{n}\}\)을 제외한 나머지 n-1개의 수를 가지고 1번의 알고리즘을 적용해서 \(x_{1},\,x_{2},\,\cdots,\,x_{n}\)중 두번째로 큰 수를 찾는다.
3. 위 과정을 반복해서 \(x_{1},\,x_{2},\,\cdots,\,x_{n}\)을 크기순으로 나열할 수 있다.
이 경우의 비교회수는 \(\displaystyle(n-1)+(n-2)+\cdots+1=\frac{n(n-1)}{2}\)이다.
방법 2
1. \(x_{1},\,x_{2},\,\cdots,\,x_{n}\) 중 임의로 \(y\)를 선택해서 나머지 \(n-1\)개의 원소들을 \(y\)를 기준으로 \(y\)보다 작으면 \(y\)의 앞에, \(y\)보다 크면 \(y\)의 뒤에 두어서 두 개의 집합 \(X_{1}\)과 \(X_{2}\)로 분리한다.
2. \(X_{1}\)과 \(X_{2}\) 각각을 1과 같은 방법을 이용하여 크기순으로 나열해 합치면 원하는 배열을 얻을 수 있다.
이 경우의 비교회수는 대부분 방법 1보다 빠른 시간안에 해결가능하나 최악의 경우는 방법 1과 같은 비교회수를 통해 문제가 해결된다.
수열의 \(n\)번째 항을 그 이웃한 항이나 그보다 앞선 항들에 대한 관계식으로 나타낼 수 있을 때가 있다.(예: 피보나치 수열 \(a_{n+2}=a_{n+1}+a_{n},\,a_{1}=a_{2}=1\)) 이러한 관계를 점화관계(recurrence relation)라고 하고 여기의 관계식을 점화식(recurrence formula)이라고 한다. 특별한 경우, 점화식과 초기조건으로부터 일반항 \(a_{n}\)의 식을 유도할 수 있다.
예: 하노이 탑 문제(Hanoi tower problem)

(하노이 탑 모형)
등판에 막대가 3개 있고, 크기가 서로 다른 \(n\)개의 원판이 한 막대에 크기순으로(큰 원판이 작은 원판보다 아래에 놓임) 꽂혀 있다. 이때 다음의 규칙대로 원판을 다른 막대로 옮긴다.
(1) 한 번에 한개의 원판만을 옮긴다.
(2) 크기가 큰 원판은 반드시 크기가 작은 원판 아래쪽에 있어야 한다.
그러면 원판을 모두 다른 막대로 옮기는데 필요한 최소한의 이동 횟수는?
풀이: 원판의 개수가 \(n\)일 때, 최소 이동횟수를 \(a_{n}\)이라 하자. 그러면\(a_{1}=1,\,a_{2}=3\)이고
임의의 \(n\)에 대하여, 가장 큰 원판을 처음으로 옮길 때에는, 다른 원판들은 모두 하나의 막대에 크기순으로 배열되어 있어야 한다. 따라서 가장 큰 원판을 옮기기 전까지의 최소 이동횟수는 \(a_{n-1}\)이다. 가장 큰 원판을 비어있는 다른 원판에 이동한 다음, 나머지 \(n-1\)개의 원판을 가장 큰 원판이 놓여 있는 막대로 이동해야 한다. 따라서 \(a_{n}=2a_{n-1}+1\)이 성립하고$$\begin{align*}a_{3}&=2a_{2}-1=7=2^{3}-1\\a_{4}&=2{a}^{3}+1=2(2^{3}-1)+1=2^{4}-1\end{align*}$$이므로 \(a_{n}=2^{n}-1\)이다.
(\(n=4\)일 때, \(a_{4}=2^{4}-1=15\)이다)
*참고: 베트남 하노이 시 외곽에 있는 베나레스(Benares) 사원의 한 가운데에 있는 돔(Dome)에 다음의 전설이 기록된 동판이 있다:
"동판에 다이아몬드 막대가 3개 있고, 크기가 서로 다른 64개의 황금 원판이 한 막대에 꽂혀있다. 이때 다음과 같은 규칙으로 황금 원판을 다른 막대로 모두 옮기는 놀이를 신(god, 神)이 하고 있다
(1) 한번에 한개의 황금원판만을 옮긴다.
(2) 크기가 큰 황금원판은 반드시 크기가 작은 황금 원판 아래에 있어야 한다.
신이 이 놀이를 끝내면(황금원판이 다른 막대로 모두 옮겨졌다면), 이 세상은 종말이 올 것이다."
실제로 황금원판 한개를 다른 원판으로 옮기는데 1초가 걸린다고 가정하면, 황금원판이 다른 막대로 모두 옮겨지는데 걸리는 시간은 \(2^{64}-1=18,446,744,073,709,551,615\)초(대략 5833억년)가 걸린다.(걱정할 필요가 없다)
예: 한 아이가 7개의 계단을 올라간다고 하자. 이때 한번에 하나 또는 두개의 계단을 오를 수가 있다. 이 아이가 7개의 계단을 서로 다르게 오르는 방법의 수는?
풀이: \(n\)개의 계단을 오르는 경우의 수를 \(a_{n}\)이라 하자. 그러면 \(a_{1}=1,\,a_{2}=2\)익, \(n\geq3\)인 경우, 처음에 한 개의 계단을 오르는 경우, 이 경우의 수는 남아있는 \(n-1\)개의 계단을 오르는 방법의 수와 같으므로 \(a_{n-1}\)가지가 된다. 처음에 두개를 오르는 경우, 남아있는 \(n-2\)개의 계단을 오르는 방법의 수와 같으므로 \(a_{n-2}\)가지가 된다. 따라서 다음의 점화식$$a_{n}=a_{n-1}+a_{n-2}\,(a_{1}=1,\,a_{2}=2,\,n\geq3)$$을 얻고$$a_{7}=a_{6}+a_{5}=2a_{5}+a_{4}=3a_{4}+2a_{3}=5a_{3}+3a_{2}=8a_{2}+5a_{1}=16+5=21$$이다.
참고: 위의 점화식을 갖는 수열을 피보나치 수열(Fibonacci sequence)이라고 한다.
예: 평면상에 \(n\)개의 직선이 나누는 영역의 최대 개수(어떤 두 직선도 평행하지 않고, 어떤 세 직선도 한 점에서 만나지 않도록 직선을 그을 때 생기는 영역의 수)는?
풀이: \(n\)개의 직선으로 나눌 때 생기는 영역의 최대 개수를 \(a_{n}\)이라고 하자. 그러면 \(a_{1}=2\)이고 \(n\geq2\)일 때, \(n\)번째 직선을 그리면 나머지 \(n-1\)개의 직선과 만나는 교점의 수는 \(n-1\)개이고, 영역의 수는 \(n\)개 더 늘어난다. 따라서 점화식$$a_{n}=a_{n-1}+n,\,a_{1}=2\,(n\geq2)$$을 얻고 일반항은$$a_{n}=1+\frac{n(n+1)}{2}$$이다.
예: \(0,\,1,\,2\)로 이루어진 길이가 \(n\)인 \(3^{n}\)개의 수열 중 \(0\)의 개수가 홀수인 수열의 개수는?
풀이: 길이가 \(n\)이고 \(0\)의 개수가 홀수인 수열의 개수를 \(b_{n}\)이라고 하자.
끝자리가 \(1\)인 경우는 \(b_{n-1}\)개 이고, 끝자리가 \(2\)인 경우는 \(b_{n-1}\)개, 끝자리가 \(0\)인 경우, \(3^{n-1}-b_{n-1}\)이므로 다음의 점화식을 얻고$$b_{n}=b_{n-1}+3^{n-1},\,b_{1}=1$$이므로 \(\displaystyle b_{n}=\frac{3^{n}-1}{2}\)이다.
참고자료:
조합론과 그래프이론, 조성진, 김한두, 경문사
https://www.scienceall.com/%EC%88%9C%EC%84%9C%EB%8F%84flow-chart/
https://support.office.com/ko-kr/article/%EA%B8%B0%EB%B3%B8-%EC%88%9C%EC%84%9C%EB%8F%84-%EB%A7%8C%EB%93%A4%EA%B8%B0-e207d975-4a51-4bfa-a356-eeec314bd276
https://en.wikipedia.org/wiki/Tower_of_Hanoi
수학비타민, 박경미, 랜덤하우스 중앙
'확률및통계 > 조합론' 카테고리의 다른 글
| [조합론] 6. 점화식(3: 생성함수) (0) | 2019.03.04 |
|---|---|
| [조합론] 5. 점화식(2: 선형점화식) (0) | 2019.03.03 |
| [조합론] 3. 경우의 수 세기(2: 중복순열, 중복조합, 이항계수의 성질) (0) | 2019.03.01 |
| [조합론] 2. 경우의 수 세기(1: 순열, 조합) (0) | 2019.02.28 |
| [조합론] 1. 조합론의 정의와 여러가지 증명방법 (0) | 2019.02.27 |